Core Practical 16: Investigating Resonance (Edexcel International A Level (IAL) Physics): Revision Note

Core Practical 16: Investigating Resonance

Aim of the Experiment

• Determine the value of an unknown mass by a graphical method by using the resonant frequencies of the oscillation of known masses

Variables

• Independent variable = mass (kg)

• Dependent variable = time period (s)

• Control variables:

  • The spring / oscillator

Equipment

• Spring (standard 20-25 mm spring)

• Slotted 100g masses and hanger

• Retort stand and clamp

• Digital timer

• Unknown test mass

• Digital scales

Method

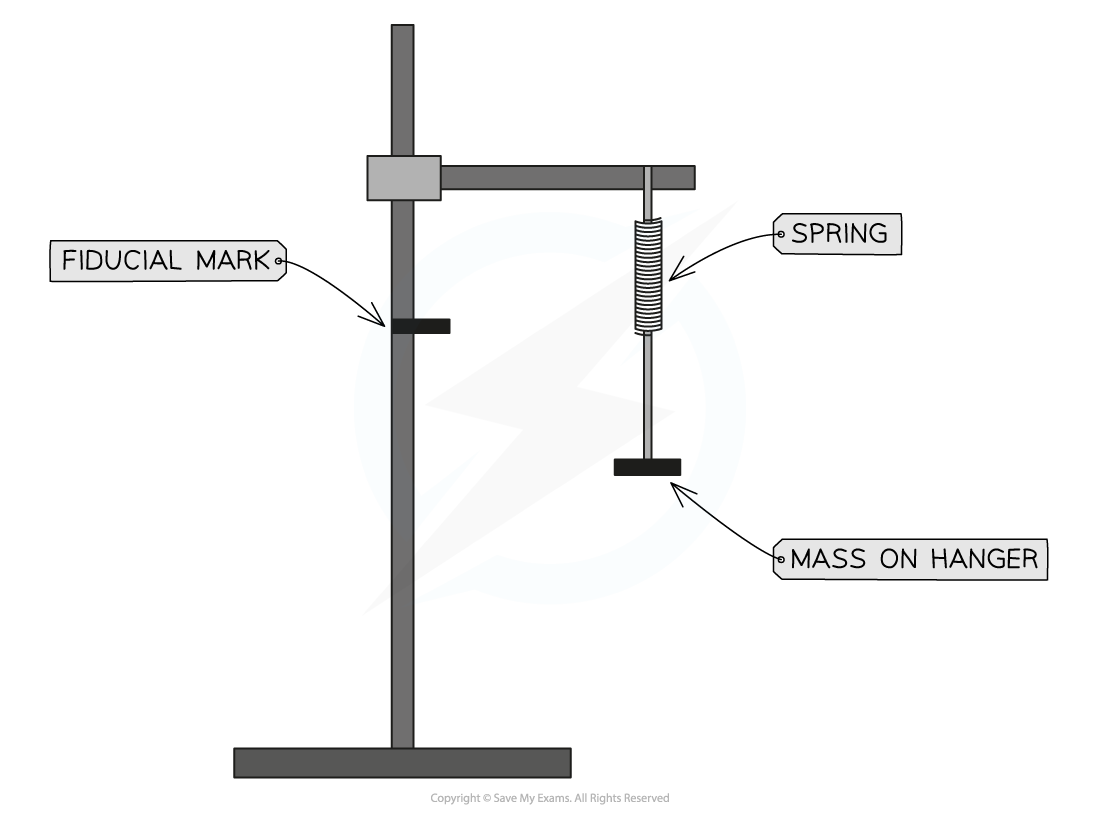
1. Set up the spring with 100 g mass attached

2. On the stand make a clear fiducial mark about 5 cm below the bottom of the spring

3. Extend the spring so that the bottom is level with the fiducial marker, release and start timing

4. Measure time for 10 oscillations

5. Repeat with the same mass two more times

6. Find the average time period of one oscillation

7. Add 100 g and adjust the fiducial mark downwards so that it is 5 cm below the new level of the spring

8. Repeat steps 3-7 until the total mass is 500 g

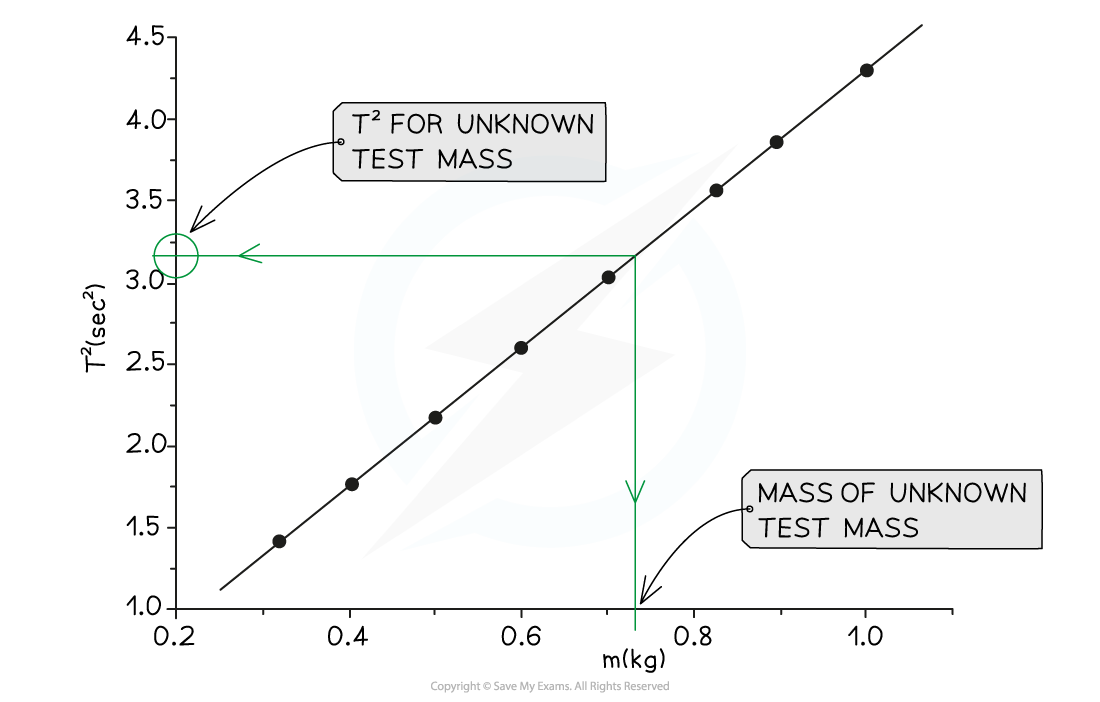
9. Plot a graph of T² on the y-axis against m on the x-axis 

Testing the unknown mass

• Follow steps 2 - 6 for the test mass

• Find the value of the time period, T and square it to find T²

• On the graph mark a horizontal from T² to the graph line and where they intersect, take the arrow vertically down to meet the x-axis

• The value of m which this line coincides with is the mass of the test mass

• Check the result using digital scales

Analysis

• Analysis for this graph is based on three equations related to simple harmonic motion;

  • Angular velocity, $\omega =\sqrt{\frac{k}{m}}$ (equation 1)

  • Where k = spring constant (N kg⁻¹) and m = mass (kg) 

  • Angular velocity, $\omega =2\mathrm{\pi f}$  (equation 2)

  • Where f = frequency of oscillations (Hz) 

  • Frequency, $f=\frac{1}{T}$ (equation 3)

  • Where T = time period for one oscillation (s) 

• Substitute equations 2 into equation 1;

$2\mathrm{\pi }f=\sqrt{\frac{k}{m}}$

• Substitute equation 3 into equation 2

$\frac{2\mathrm{\pi }}{T}=\sqrt{\frac{k}{m}}$

• Square both sides

$\frac{4{\mathrm{\pi }}^2}{T^2}=\frac{k}{m}$

• Make T² the subject

$T^2=m\left(\frac{4{\pi }^2}{k}\right)$

• Plot a graph of T² on the y-axis against m on the x-axis to get a straight line through the origin with;

gradient = $\left(\frac{4{\pi }^2}{k}\right)$

Safety Considerations

• Clamp stand to the desk for stability

• Wear safety glasses in case the spring flies off or snaps

• Place a cushion or catch-mat in case of falling masses