Equations for Nuclear Physics (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Activity & The Decay Constant
Since radioactive decay is spontaneous and random, it is useful to consider the average number of nuclei which are expected to decay per unit time
This is known as the average decay rate
As a result, each radioactive element can be assigned a decay constant
The decay constant λ is defined as:
The probability, per second, that a given nucleus will decay
When a sample is highly radioactive, this means the number of decays per unit time is very high
This suggests it has a high level of activity
Activity, or the number of decays per unit time can be calculated using:
Where:
A = activity of the sample (Bq)
ΔN = number of decayed nuclei
Δt = time interval (s)
λ = decay constant (s-1)
N = number of nuclei remaining in a sample
The activity of a sample is measured in Becquerels (Bq)
An activity of 1 Bq is equal to one decay per second, or 1 s-1
This equation shows:
The greater the decay constant, the greater the activity of the sample
The activity depends on the number of undecayed nuclei remaining in the sample
The minus sign indicates that the number of nuclei remaining decreases with time - however, for calculations it can be omitted
Worked Example
Americium-241 is an artificially produced radioactive element that emits α-particles. A sample of americium-241 of mass 5.1 μg is found to have an activity of 5.9 × 105 Bq.
(a) Determine the number of nuclei in the sample of americium-241.
(b) Determine the decay constant of americium-241.
Answer:
Part (a)
Step 1: Write down the known quantities
Mass = 5.1 μg = 5.1 × 10-6 g
Molecular mass of americium = 241
NA = Avogadro constant
Step 2: Write down the equation relating number of nuclei, mass and molecular mass
Step 3: Calculate the number of nuclei
Part (b)
Step 1: Write the equation for activity
Activity, A = λN
Step 2: Rearrange for decay constant λ and calculate the answer
Exponential Decay
In radioactive decay, the number of nuclei falls very rapidly, without ever reaching zero
Such a model is known as exponential decay
The graph of number of undecayed nuclei and time has a very distinctive shape

Radioactive decay follows an exponential pattern. The graph shows three different isotopes each with a different rate of decay
Radioactive Decay Equation
The number of undecayed nuclei N can be represented in exponential form by the equation:
N = N0e–λt
Where:
N0 = the initial number of undecayed nuclei (when t = 0)
λ = decay constant (s-1)
t = time interval (s)
The exponential function e
The symbol e represents the exponential constant
It is approximately equal to e = 2.718
On a calculator it is shown by the button ex
The inverse function of ex is ln(y), known as the natural logarithmic function
This is because, if ex = y, then x = ln(y)
Worked Example
Strontium-90 decays with the emission of a β-particle to form Yttrium-90. The decay constant of Strontium-90 is 0.025 year-1.
Determine the activity A of the sample after 5.0 years, expressing the answer as a fraction of the initial activity A0
Answer:
Step 1: Write out the known quantities
Decay constant, λ = 0.025 year-1
Time interval, t = 5.0 years
Both quantities have the same unit, so there is no need for conversion
Step 2: Write the equation for activity in exponential form
A = A0e–λt
Step 3: Rearrange the equation for the ratio between A and A0
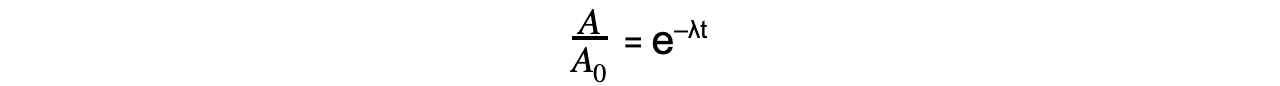
Step 4: Calculate the ratio A/A0
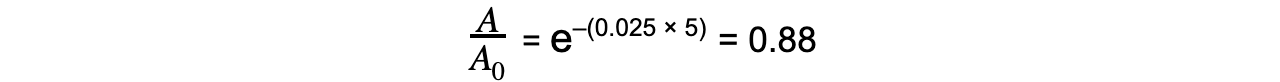
Therefore, the activity of Strontium-90 decreases by a factor of 0.88, or 12%, after 5 years
Half Life
Half-life is defined as:
The time taken for half the number of nuclei in a sample to decay
This means when a time equal to the half-life has passed, the activity of the sample will also half
This is because the activity is proportional to the number of undecayed nuclei, A ∝ N
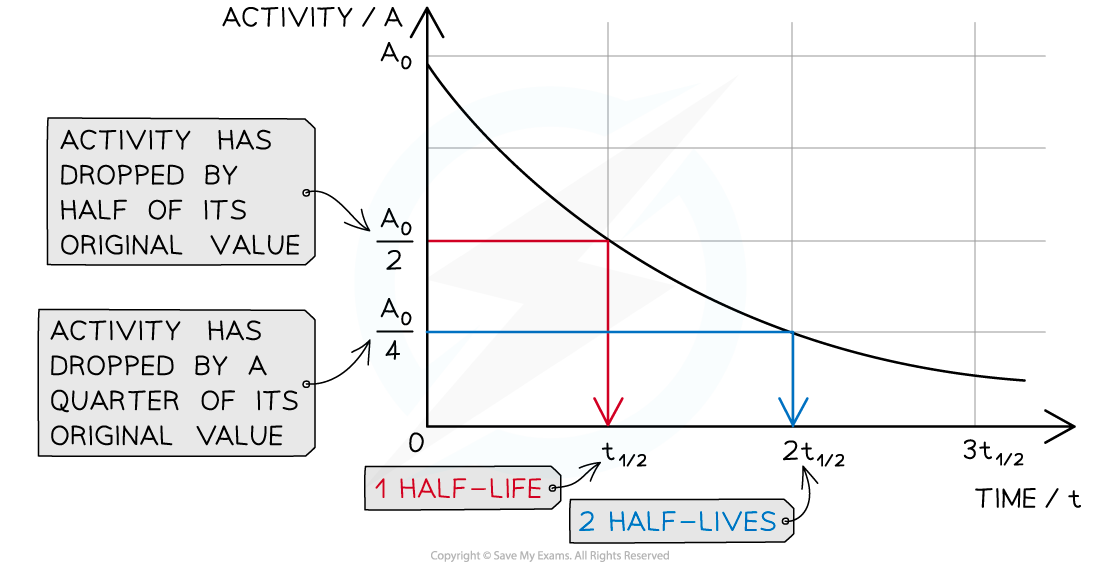
When a time equal to the half-life passes, the activity falls by half, when two half-lives pass, the activity falls by another half (which is a quarter of the initial value)
To find an expression for half-life, start with the equation for exponential decay:
N = N0 e–λt
Where:
N = number of nuclei remaining in a sample
N0 = the initial number of undecayed nuclei (when t = 0)
λ = decay constant (s-1)
t = time interval (s)
When time t is equal to the half-life t½, the activity N of the sample will be half of its original value, so N = ½ N0
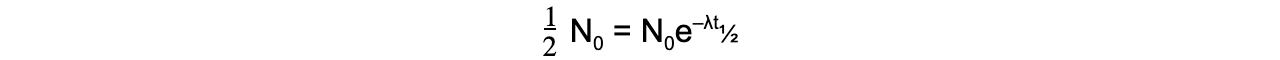
The formula can then be derived as follows:
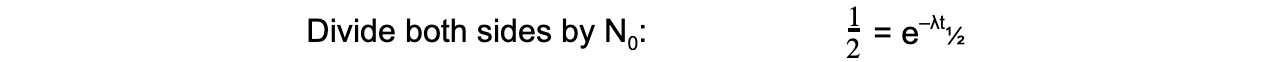


Therefore, half-life t½ can be calculated using the equation:
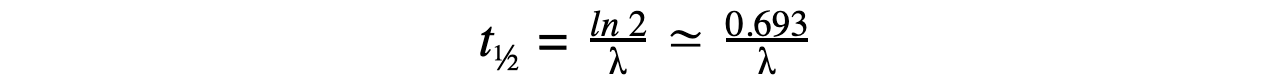
This equation shows that half-life t½ and the radioactive decay rate constant λ are inversely proportional
Therefore, the shorter the half-life, the larger the decay constant and the faster the decay
Worked Example
Strontium-90 is a radioactive isotope with a half-life of 28.0 years.A sample of Strontium-90 has an activity of 6.4 × 109 Bq. Calculate the decay constant λ, in s–1, of Strontium-90.
Answer:
Step 1: Convert the half-life into seconds
t½ = 28 years = 28 × 365 × 24 × 60 × 60 = 8.83 × 108 s
Step 2: Write the equation for half-life
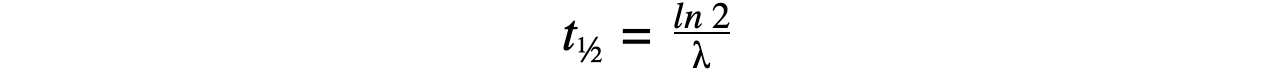
Step 3: Rearrange for λ and calculate
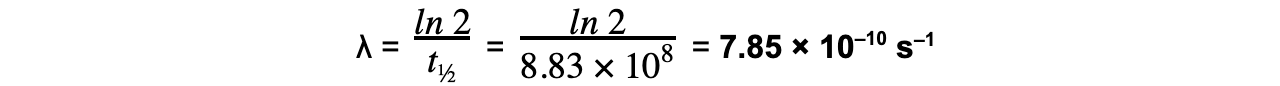
Examiner Tips and Tricks
Although you may not be expected to derive the half-life equation, make sure you're comfortable with how to use it in calculations such as that in the worked example.

Unlock more, it's free!
Did this page help you?