Gravitational Potential for a Radial Field

Near the Earth's Surface

The gravitational potential energy (G.P.E) is the energy an object has when lifted off the ground given by the familiar equation:

G.P.E = mgΔh

When using this equation, the G.P.E on the surface of the Earth is taken to be zero
- This means work is done to lift the object
This equation is only used for objects that are near the Earth's surface
- This is because, near Earth's surface, the gravitational field is approximated to be uniform
- Far away from the Earth's surface, the gravitational field is radial because the Earth is a sphere

In a Radial Field

In a radial field, G.P.E is defined as:

The energy an object possesses due to its position in a gravitational field

The gravitational potential at a point is the gravitational potential energy per unit mass at that point
Gravity is always attractive, so work must be done on a mass to move it away to a point infinitely far away from every other mass
- 'Infinity' is the point at which the gravitational potential is zero
- Therefore, since the potential energy of all masses increases as work is done on them to move them infinitely far away, the value of the potential is always negative

Gravitational potential energy is defined as:

The work done per unit mass in bringing a test mass from infinity to a defined point

It is represented by the symbol, V and is measured in J kg^–¹

Gravitational potential V_grav can be calculated at a distance r from a mass M using the equation:

$V_{g r a v} = - \frac{G M}{r}$

Where:
- V_grav = gravitational potential (J kg^–¹)
- G = Newton’s gravitational constant
- M = mass of the body producing the gravitational field (kg)
- r = distance from the centre of the mass to the point mass (m)

This means that the gravitational potential is negative on the surface of a mass (such as a planet), and increases with distance from that mass (becomes less negative)
Work has to be done against the gravitational pull of the planet to take a unit mass away from the planet
The gravitational potential at a point depends on the mass of the object producing the gravitational field and the distance the point is from that mass

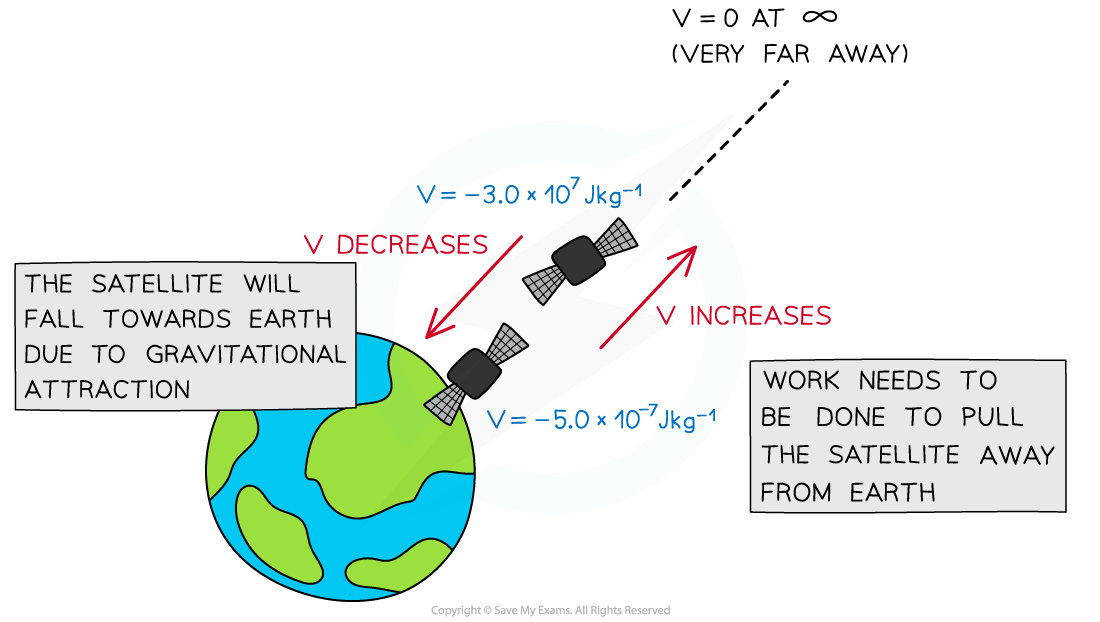
Gravitational Potential, downloadable AS & A Level Physics revision notes

Gravitational potential decreases as the satellite moves closer to the Earth

Worked example

Calculate gravitational potential at the surface of Mars.

Radius of Mars = 3400 km

Mass of Mars = 6.4 × 10²³ kg

Step 1: Write the gravitational potential equation

$V_{g r a v} = - \frac{G M}{r}$

Step 2: Substitute known quantities

$V_{g r a v} = - \frac{(6.67 \times 10^{- 11}) \times (6.4 \times 10^{23})}{3400 \times 10^{3}}$ = –1.3 × 10⁷ J kg^–1

Examiner Tip

The equation for gravitational potential in a radial field looks very similar to the equation for gravitational field strength in a radial field, but there is a very important difference! Remember, for gravitational potential:

$V_{g r a v} = - \frac{G M}{r}$ so $V_{g r a v} \propto \frac{1}{r}$

However, for gravitational field strength:

$g = \frac{G M}{r^{2}}$ so $g \propto \frac{1}{r^{2}}$

Additionally, remember that both V_grav and g are measured from the centre of the mass M causing the field!

Gravitational Potential for a Radial Field (Edexcel International A Level Physics)

Revision Note