Inverse Square Law of Flux (Edexcel International A Level Physics)

• The moment the light leaves the surface of the star, it begins to spread out uniformly through a spherical shell
  • Light sources which are further away appear fainter because the emitted light has been spread over a greater area
• The surface area of a sphere is equal to 4πr²
  • The radius r of this sphere is equal to the distance d between the star and the Earth
  • Therefore the radiation received at Earth has been spread over an area of 4πd²

• The inverse square law of flux can therefore be calculated using:

• Where:
  • F = radiant flux intensity, or observed intensity on Earth (W m^-2)
  • L = luminosity of the source (W)
  • d = distance between the star and the Earth (m)

• This equation assumes:
  • The power from the star radiates uniformly through space
  • No radiation is absorbed between the star and the Earth

• This equation tells us:
  • For a given star, the luminosity is constant
  • The radiant flux follows an inverse square law
  • The greater the radiant flux (larger F) measured, the closer the star is to the Earth (smaller d)

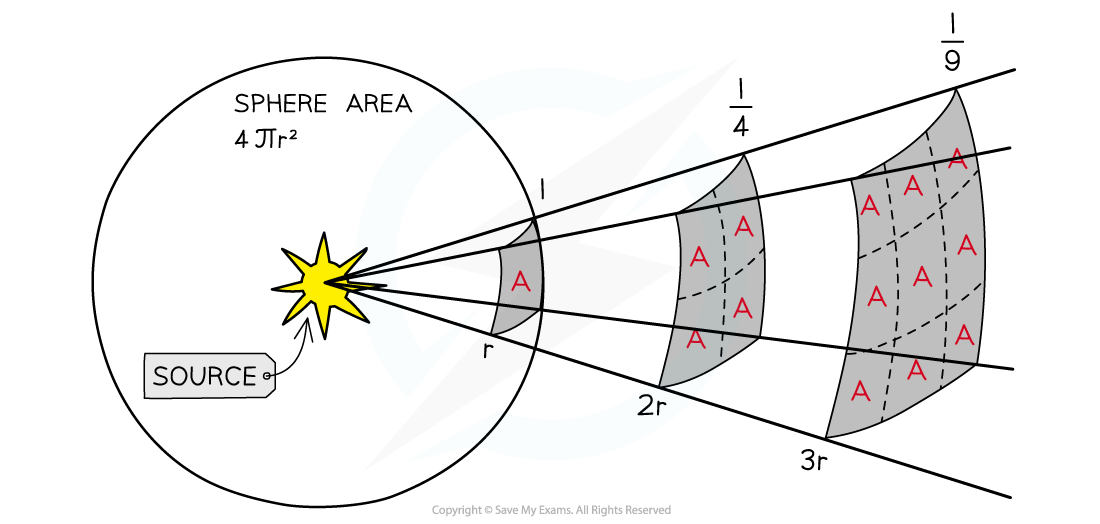
Inverse square law; when the light is twice as far away, it has spread over four times the area, hence the intensity is four times smaller

Step 1: Write down the known quantities

Luminosity, L = 4.8 × 10²⁹ W

Radiant flux intensity, F = 2.6 nW m^–2 = 2.6 × 10^–9 W m^–2

 Step 2: Write down the inverse square law of flux

Step 3: Rearrange for distance d, and calculate