Faraday & Lenz's Law (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Written by: Katie M
Updated on
Faraday and Lenz's Law
Faraday's Law
Faraday's Law connects the rate of change of flux linkage with induced e.m.f
It is defined in words as:
The magnitude of the induced e.m.f is directly proportional to the rate of change of magnetic flux linkage
Faraday's Law as an equation is defined as:
Where:
ε = induced e.m.f (V)
Δ(Nɸ) = change in flux linkage (Wb turns)
Δt = time interval (s)
If the interval of time becomes very small (i.e., in the limit of Δt → 0) the equation for Faraday's Law can be written as:
Lenz's Law
Lenz’s Law is used to predict the direction of an induced e.m.f in a coil or wire
Lenz's Law is summarised below:
The induced e.m.f is set up in a direction to produce effects that oppose the change causing it
Lenz's Law can be experimentally verified using:
A bar magnet
A coil of wire
A sensitive ammeter
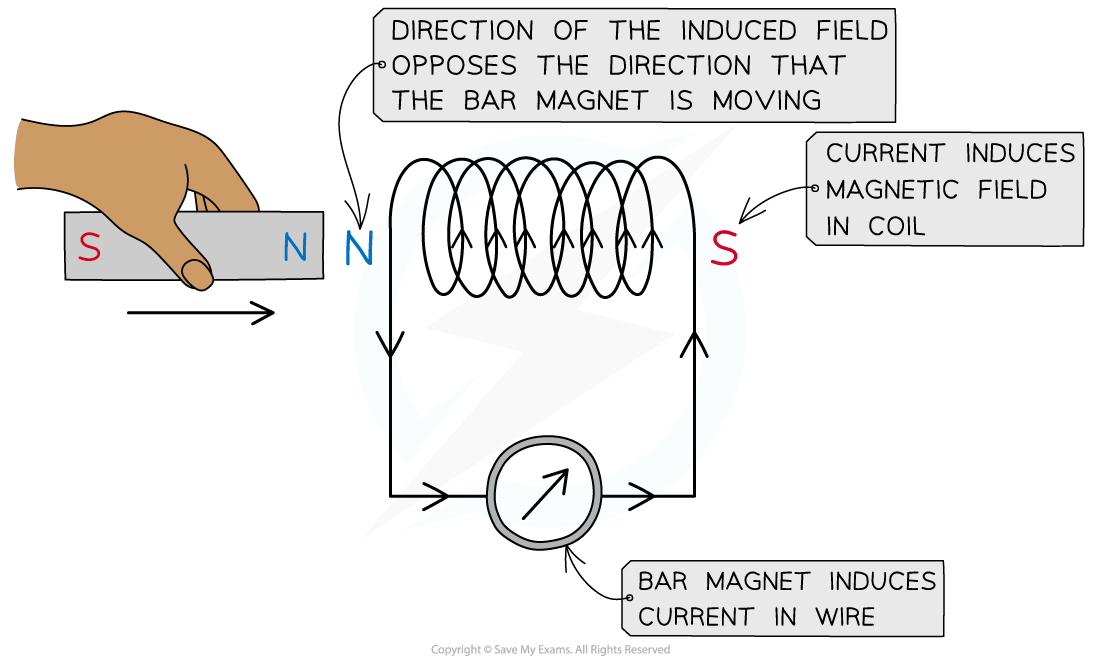
Lenz’s law can be verified using a coil connected in series with a sensitive ammeter and a bar magnet
A known pole (either north or south) of a bar magnet is pushed into the coil
This induces an e.m.f in the coil
The induced e.m.f drives a current (because it is a complete circuit)
Lenz's Law dictates:
The direction of the e.m.f, and hence the current, must be set up to oppose the incoming magnet
Since a north pole approaches the coil face, the e.m.f must be set up to create an induced north pole
This is because two north poles will repel each other
The direction of the current is therefore as shown in the image above
The direction of current can be verified using the right hand grip rule
Fingers curl around the coil in the direction of current and the thumb points along the direction of the flux lines, from north to south
Therefore, the current flows in an anti-clockwise direction in the image shown, in order to induce a north pole opposing the incoming magnet
Combining Lenz's Law and Faraday's Law
Combining Lenz's Law into the equation for Faraday's Law is written as:
The negative sign represents Lenz's Law
This is because it shows the induced e.m.f ε is set up in an 'opposite direction' to oppose the changing flux linkage
This equation also shows that the gradient of the graph of magnetic flux (linkage) against time,
represents the magnitude of the induced e.m.f
Note: the negative sign means if the gradient is positive, the induced e.m.f is negative
This is again due to Lenz's Law, which says the e.m.f is set up to oppose the effects of the changing flux linkage
Worked Example
A small rectangular coil contains 350 turns of wire. The longer sides are 3.5 cm and the shorter sides are 1.4 cm.
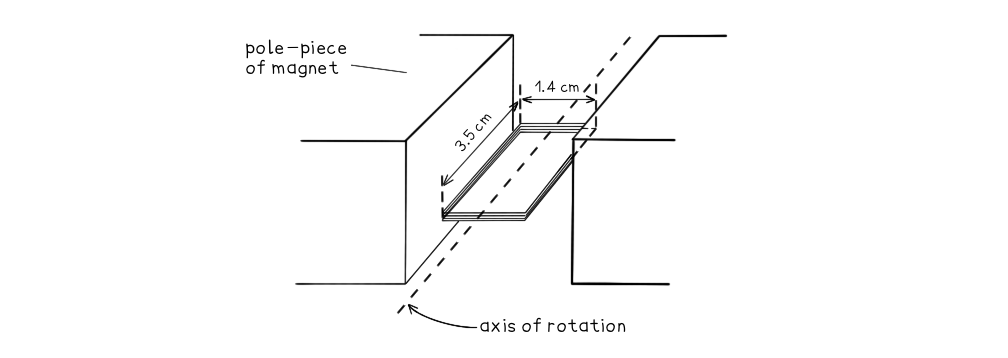
The coil is held between the poles of a large magnet so that it can rotate about an axis through its centre. The magnet produces a uniform magnetic field of flux density 80 mT between its poles. The coil is positioned horizontally and then turned through an angle of 90° in a time of 0.18 s.
Calculate the magnitude of the average e.m.f induced in the coil.
Answer:
Step 1: Write down the known quantities
Magnetic flux density, B = 80 mT = 80 × 10-3 T
Area, A = 3.5 × 1.4 = (3.5 × 10-2) × (1.4 × 10-2) = 4.9 × 10-4 m2
Number of turns, N = 350
Time interval, Δt = 0.18 s
Step 2: Write out the equation for Faraday’s law:
Step 3: Write out the equation for the change in flux linkage:
The number of turns N and the coil area A stay constant
The flux through the coil changes as it rotates
Therefore, the change in flux linkage can be written as:
Δ(NΦ) = NA(ΔB)
Step 4: Determine the change in magnetic flux linkage
The initial flux through the coil is zero (flux lines are parallel to the coil face)
The final flux through the coil is 80 mT (flux lines are perpendicular to the coil face)
This is because the coil begins horizontally in the field and is rotated 90°
Therefore, the change in flux linkage is:
Δ(NΦ) = NA(ΔB) = 350 × (4.9 × 10-4) × (80 × 10-3) = 0.014 Wb turns
Step 5: Substitute change in flux linkage and time into Faraday’s law equation:
= 0.076 V
Examiner Tips and Tricks
The 'magnitude' of the e.m.f just means its size, rather than its direction. This is often what is required in exam questions, so the minus sign in Lenz's law is not necessarily required in calculations. However, you may be expected to explain the significance of the negative sign in the equation, so be prepared to interpret it as an expression of Lenz's Law!
Remember that 'd' and the greek letter delta, 'Δ', simply mean 'change in'.

Unlock more, it's free!
Was this revision note helpful?
