Magnetic Flux Density, Flux & Flux Linkage (Edexcel International A Level Physics)

Magnetic Flux, Flux Density & Flux Linkage

Magnetic Flux Density

• The strength of a magnetic field is defined by the density of the magnetic field lines, or magnetic flux density, at that point

  • Magnetic flux density is defined by the symbol B

  • It is measured in Tesla (T)

• Rearranging the equation for magnetic force on a wire, the magnetic flux density is defined by the equation:

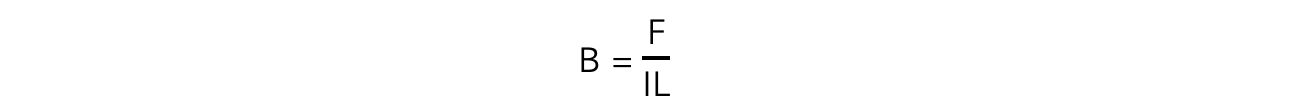
• Where:

  • B = magnetic flux density (T)

  • F = magnetic force on a current-carrying wire (N)

  • I = current (A)

  • L = length of the wire (m)

• For reference, the Earth's magnetic flux density is around 0.032 mT and an ordinary fridge magnet is around 5 mT

• The magnetic flux density is sometimes referred to as the magnetic field strength

Magnetic Flux

• Magnetic flux is a quantity which signifies how much of a magnetic field passes perpendicularly through some area

• For example, the amount of magnetic flux through a rotating coil will vary as the coil rotates in the magnetic field

  • It is a maximum when the magnetic field lines are perpendicular to the coil area

  • It is at a minimum when the magnetic field lines are parallel to the coil area

• The magnetic flux is defined as:

  The product of the magnetic flux density and the cross-sectional area perpendicular to the direction of the magnetic flux density

• Magnetic flux is defined by the symbol Φ (greek letter ‘phi’)

• It is measured in units of Webers (Wb)

• Magnetic flux can be calculated using the equation:

Φ = BA

• Where:

  • Φ = magnetic flux (Wb)

  • B = magnetic flux density (T)

  • A = cross-sectional area (m²)

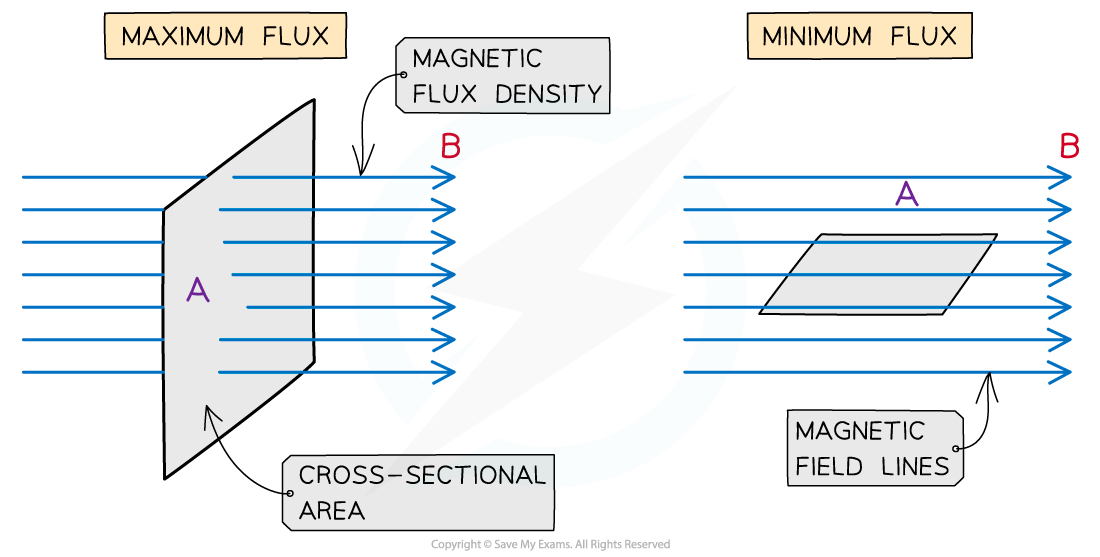
The magnetic flux is maximised when the magnetic field lines and the area through which they are passing through are perpendicular

• When magnetic flux is not completely perpendicular to the area A, then the component of magnetic flux density B perpendicular to the area is taken

• The equation then becomes:

Φ = BA cos(θ)

• Where:

  • θ = angle between magnetic field lines and the line perpendicular to the plane of the area (often called the normal line) (degrees)

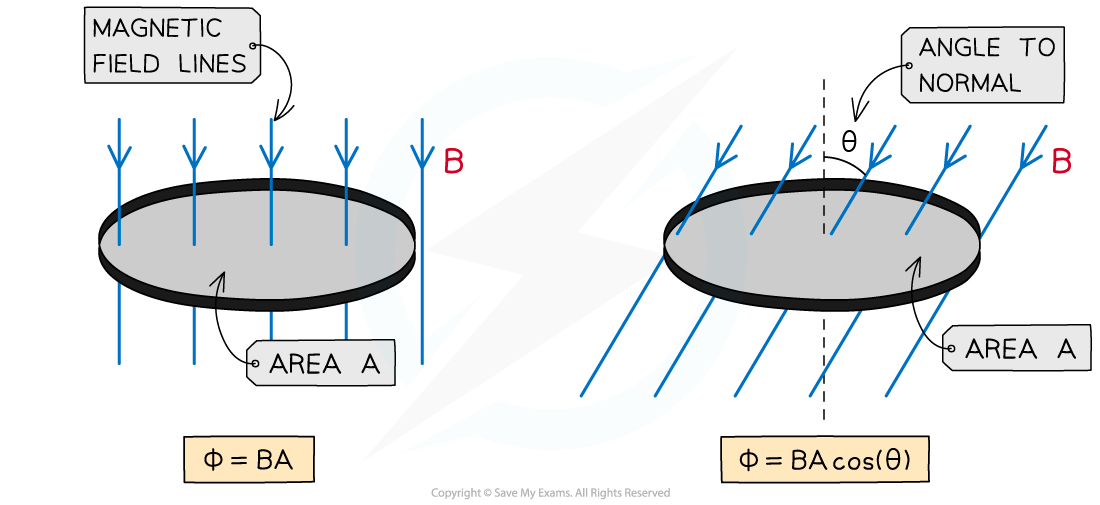
The magnetic flux increases as the angle between the field lines and the normal decreases

• This means the magnetic flux is:

  • Maximum = BA when cos(θ) =1 therefore θ = 0^o. The magnetic field lines are perpendicular to the plane of the area

  • Minimum = 0 when cos(θ) = 0 therefore θ = 90^o. The magnetic fields lines are parallel to the plane of the area

• An e.m.f is induced in a circuit when the magnetic flux linkage changes with respect to time

• This means an e.m.f is induced when there is:

  • A changing magnetic flux density B

  • A changing cross-sectional area A

  • A change in angle θ

Magnetic Flux Linkage

• The magnetic flux linkage is a quantity commonly used for solenoids which are made of N turns of wire

• The flux linkage is defined as:

  The product of the magnetic flux and the number of turns of the coil

• It is calculated using the equation:

Flux linkage = ΦN = BAN

• Where:

  • Φ = magnetic flux (Wb)

  • N = number of turns of the coil

  • B = magnetic flux density (T)

  • A = cross-sectional area (m²)

• The flux linkage ΦN has the units of Weber turns (Wb turns)