Relativistic Situations (Edexcel International A Level Physics)

• Accelerated particles often reach speeds that are very close to the speed of light
• At such high velocities and energies, relativistic effects begin to become important
• These are effects such as:
  • Time dilation
  • Length contraction

Time Dilation

• Clocks run slower for moving particles
  • This means that unstable particles, with a short lifetime, actually survive for much longer in a laboratory if they are moving very quickly
  • This is useful because they will leave longer tracks in particle detectors (making detection easier)

• For example, muons created high up in the atmosphere, have a lifetime of about 2 μs
  
  • The time required to travel to sea-level is too great to survive the journey
  • However, they are detected at sea-level in large numbers
  • This is because they are travelling at relativistic speeds (e.g. 0.98c) so time dilation means their lifetime is dilated to times much longer than 2 μs

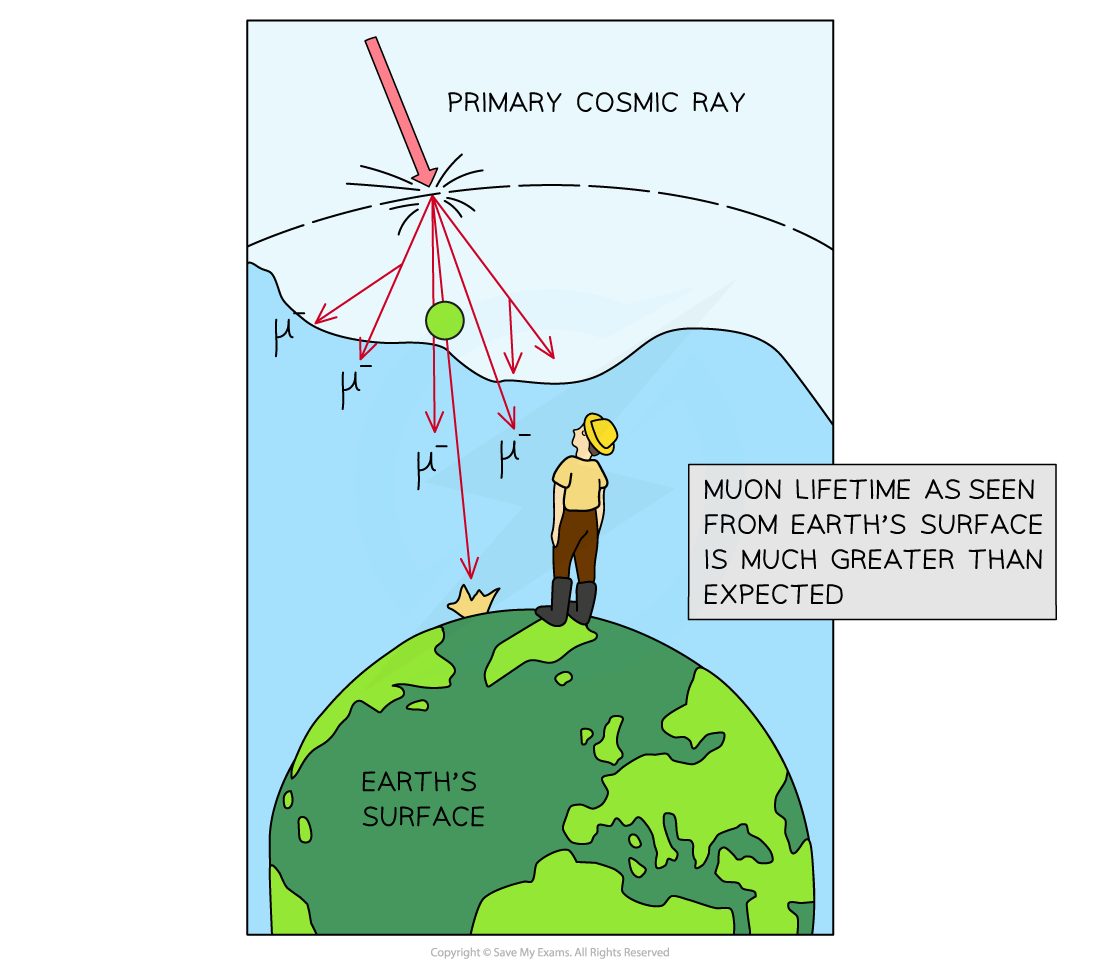
Because muons travel so quickly, time dilation stretches muon lifetime to much longer than when they are at rest

Length Contraction

• Moving rulers are shorter than stationary rulers
  • This means that particles moving at very high velocities travel much further through detectors than expected
  • Unstable particles with very short lifetimes would not travel for appreciable distances without relativistic effects like length contraction

• For example, if exotic particles produced in particle accelerators decayed within the particle chamber before escaping it, none would be detectable
  • In fact, many types of exotic particles are detected
  • This is evidence of length contraction

Part (a)

Step 1: Write the known quantities

• • Muon lifetime, t = 2.2 × 10^–6 s
  • Speed of light, c = 3 × 10⁸ m s^–1
  • Speed of muons, v = 0.99 c = 0.99 × (3 × 10⁸) = 2.97 × 10⁸ m s^–1

Step 2: Calculate distance travelled

• • Speed v = distance d ÷ time t
  • Therefore, the distance travelled by muons travelling at 0.99 c is given by:

d = vt = (2.97 × 10⁸) × (2.2 × 10^–6) = 653.4 m

Part (b)

Step 1: Compare the distance calculated to the distance required

• • The distance a muon travels with a lifetime of 2.2 × 10^–6 s is only 653.4 m 
    • This is much less than the 10 km required to sea level

Step 2: Conclude that relativistic effects must be at play

• • Therefore, time dilation must be allowing the muons to last much longer than 2.2 × 10^–6 s
    • This is because they are detected in large numbers at sea level