Representing Radial & Uniform Electric Fields (Edexcel International A Level (IAL) Physics) : Revision Note
Using Field Lines & Equipotential Diagrams
Electric field lines
Field lines are used to represent the direction and magnitude of an electric field
In an electric field, field lines are always directed from the positive charge to the negative charge
In a uniform electric field:
the field lines are equally spaced at all points
electric field strength is constant at all points in the field
the force acting on a test charge has the same magnitude and direction at all points in the field
In a radial electric field:
the field lines are equally spaced as they exit the surface of the charge but the distance between them increases with distance
the electric field strength decreases with distance from the charge producing the field
the magnitude of the force acting on a test charge decreases with distance
Electric field around a point charge
Around a point charge, the electric field is radial and the lines are directly radially inwards or outwards
If the charge is positive (+), the field lines are radially outwards
If the charge is negative (-), the field lines are radially inwards

Electric field lines around a point charge are directed away from a positive charge and towards a negative charge
A radial field spreads uniformly to (or from) the charge in all directions, and the strength of the field is indicated by the spacing of the field lines
The electric field is stronger where the lines are closer together
The electric field is weaker where the lines are further apart
This shares many similarities to radial gravitational field lines around a point mass
Since gravity is only an attractive force, the field lines will look similar to the negative point charge, whilst electric field lines can be in either direction
Electric field around a conducting sphere
When a conducting sphere becomes charged, the electric field around it is the same as it would be if all the charge was concentrated at the centre
This means that a charged sphere can be treated in the same way as a point charge in calculations

Electric field lines around a charged conducting sphere are similar to the field lines around a point charge
Note: field lines are always perpendicular to the surface of a conducting sphere
Electric field between two point charges
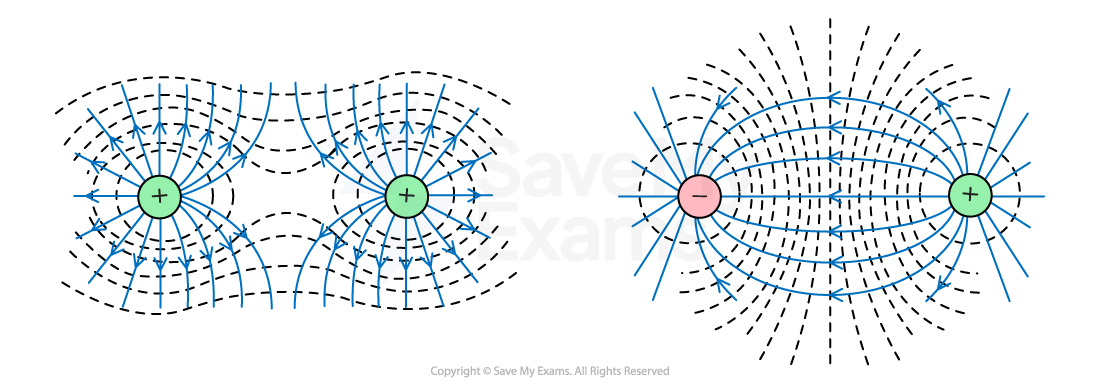
For two opposite charges:
the field lines are directed from the positive charge to the negative charge
the closer the charges are brought together, the stronger the attractive electric force between them becomes

The electric field lines between two opposite charges are directed from the positive to the negative charge. The field lines connect the surfaces of the charges to represent attraction
For two charges of the same type:
the field lines are directed away from two positive charges or towards two negative charges
the closer the charges are brought together, the stronger the repulsive electric force between them becomes
there is a neutral point at the midpoint between the charges where the resultant electric force is zero

The electric field lines between two like charges are directed away from positive charges or towards negative charges. The field lines do not connect the surfaces of the charges to represent repulsion
Electric field between two parallel plates
When a potential difference is applied between two parallel plates, they become charged
The electric field between the plates is uniform
The electric field beyond the edges of the plates is non-uniform

Electric field lines between two parallel plates are directed from the positive to the negative plate. A uniform electric field has equally spaced field lines
Electric field between a point charge and parallel plate
The field around a point charge travelling between two parallel plates combines
the field around a point charge
the field between two parallel plates

The electric field lines between a point charge and a parallel plate are similar to the field between two opposite charges. The field lines become parallel when they touch the plate
Equipotential diagrams
Equipotential lines (2D) and surfaces (3D) join together points that have the same electric potential
These are always:
perpendicular to the electric field lines in both radial and uniform fields
represented by dotted lines (unlike field lines, which are solid lines with arrows)
an equal distance from the source charge
Equipotential surfaces can be drawn to represent a fixed electric potential for a number of scenarios, such as
for a point charge
for two or more charges
between two oppositely charged parallel plates
Equipotential surface for a point charge
In a radial field, such as around a point charge, the equipotential lines:
are concentric circles around the charge
become progressively further apart with distance
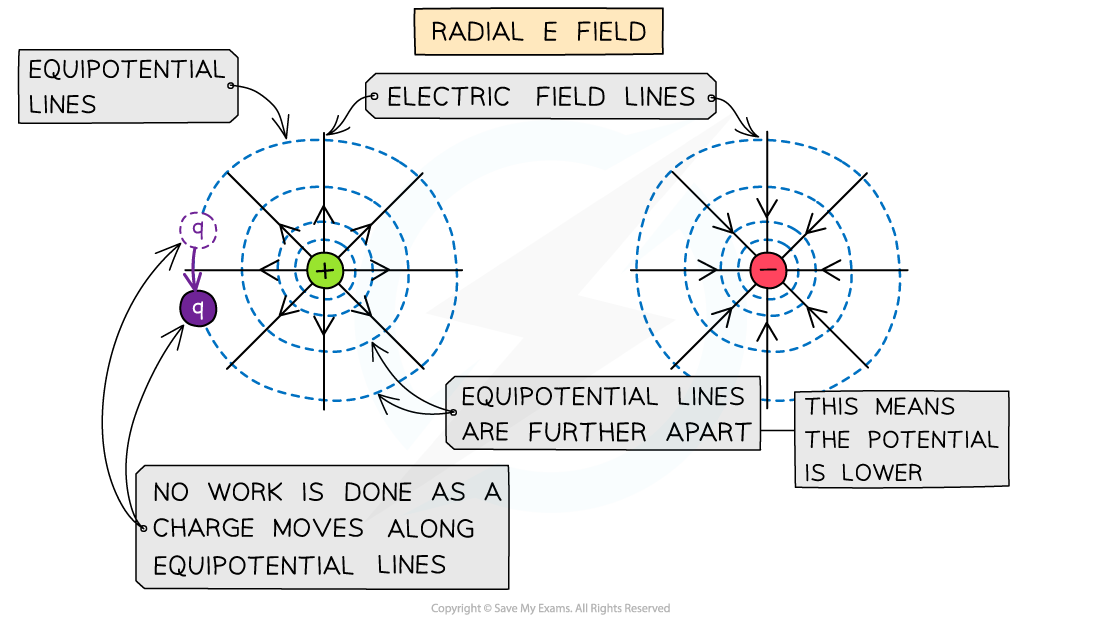
Equipotential lines for a radial electric field are concentric circles which increase in radius and are perpendicular to the field lines
If a charged conducting sphere replaced a point charge, the equipotential surface would be the same
Equipotential surface for multiple charges
The equipotential surfaces for a dipole (two opposite charges) and for two like charges are shown below:
The equipotential surface for multiple charges can be obtained by drawing curves which are perpendicular to the field lines
An equipotential surface between two opposite charges can be identified by a central line at a potential of 0 V
This is the point where the opposing potentials cancel
An equipotential surface between two like charges can be identified by a region of empty space between them
This is the point where the resultant field is zero
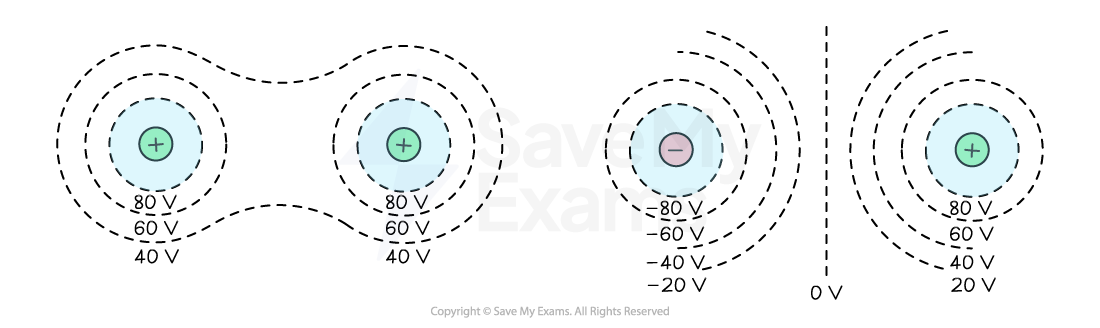
Equipotential lines show that the potential has the greatest value near the charge and decreases with distance
Equipotential surface between parallel plates
In a uniform field, such as between two parallel plates, the equipotential lines are:
horizontal straight lines
parallel
equally spaced
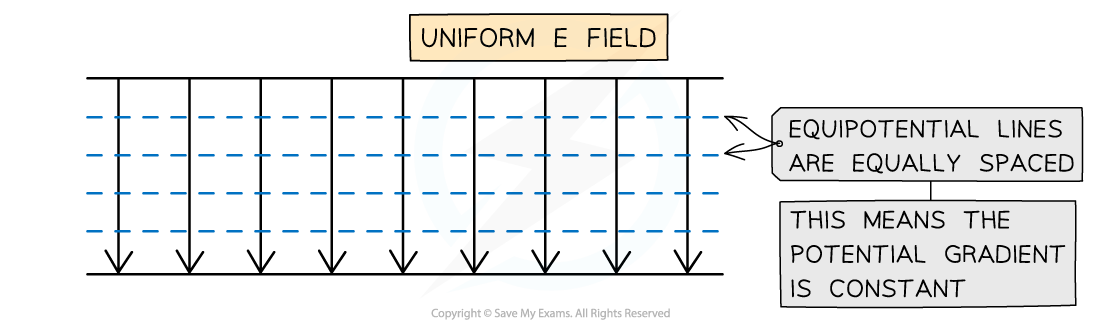
The equipotential lines for a uniform field are evenly spaced parallel lines which are perpendicular to the field lines
The spacing between equipotential lines indicates the strength of the electric field
This is because they represent potential gradient
Hence, equally spaced equipotential lines indicate a region of constant electric field strength
Worked Example
Sketch the electric field lines between the two point charges in the diagram below.

Answer:
Electric field lines around point charges have arrows which point radially outwards for positive charges and radially inwards for negative charges
Arrows (representing force on a positive test charge) point from the positive charge to the negative charge

Worked Example
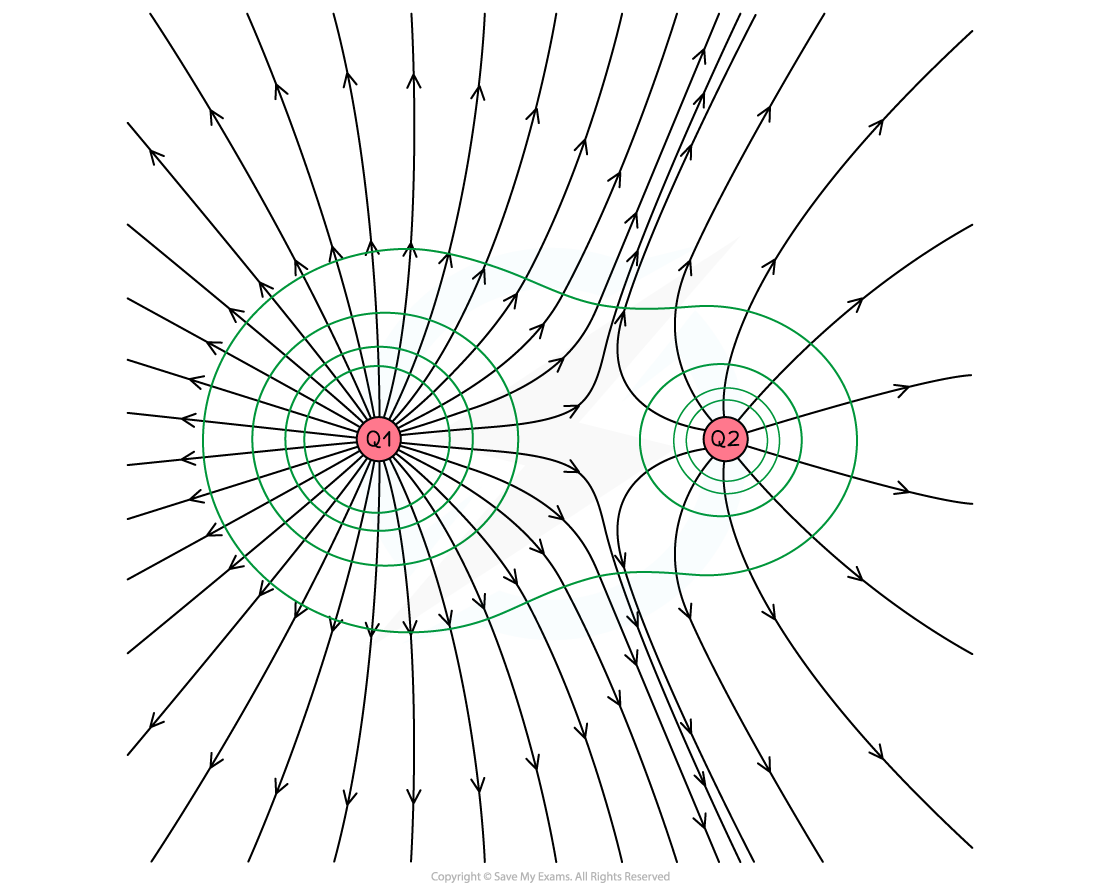
In the following diagram, two electric charges are shown which include the electric field lines

(a) Draw the lines of equipotential including at least four lines and at least one that encircles both charges
(b) By considering the field lines and equipotentials from part (a), state what can be assumed about the two charges
Answer:
Part (a)
The lines of equipotential need to be perpendicular to the field lines at all times
These lines are almost circular when they are near the charges
And when moving out further the lines of equipotential cover both charges.
The lines of equipotential can be seen below
Part (b)
It can be assumed that both charges are positive since the field lines point outwards.
It can also be assumed that the charge on the left has a larger charge than the charge on the right since:
It has a greater density of field lines
It has a larger sphere of influence shown by the lines of equipotential
The point of zero electric field strength between the two charges is closer to the right charge
Examiner Tips and Tricks
Always label the arrows on the field lines! The lines must also touch the surface of the source charge or plates and they must never cross.
The distinction between radial and uniform fields is an important one, remember:
a radial field is made up of lines which follow the radius of a circle
a uniform field is made up of lines which are a uniform distance apart
When drawing equipotential lines, remember that they do not have arrows since they have no particular direction and are not vectors.

You've read 1 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

