Electric Potential for a Radial Field (Edexcel International A Level Physics)

Electric Potential Energy

• In order to move a positive charge closer to another positive charge, work must be done to overcome the force of repulsion between them
  • Similarly, to move a positive charge away from a negative charge, work must be done to overcome the force of attraction between them

• Energy is therefore transferred to the charge that is being pushed upon
  • This means its potential energy increases

• If the positive charge is free to move, it will start to move away from the repelling charge
  • As a result, its potential energy decreases back to 0

• This is analogous to the gravitational potential energy of a mass increasing as it is being lifted upwards and decreasing as it falls
• The electric potential at a point is defined as:

The work done per unit charge in bringing a positive test charge from infinity to that point

• Electric potential is a scalar quantity
  • This means it doesn’t have a direction

• However, you will still see the electric potential with a positive or negative sign. This is because the electric potential is:
  • Positive around an isolated positive charge
  • Negative around an isolated negative charge
  • Zero at infinity

• Positive work is done to move a positive test charge from infinity to a point around a positive charge and negative work is done to move it to a point around a negative charge. This means:
  • When a positive test charge moves closer to a negative charge, its electric potential decreases
  • When a positive test charge moves closer to a positive charge, its electric potential increases

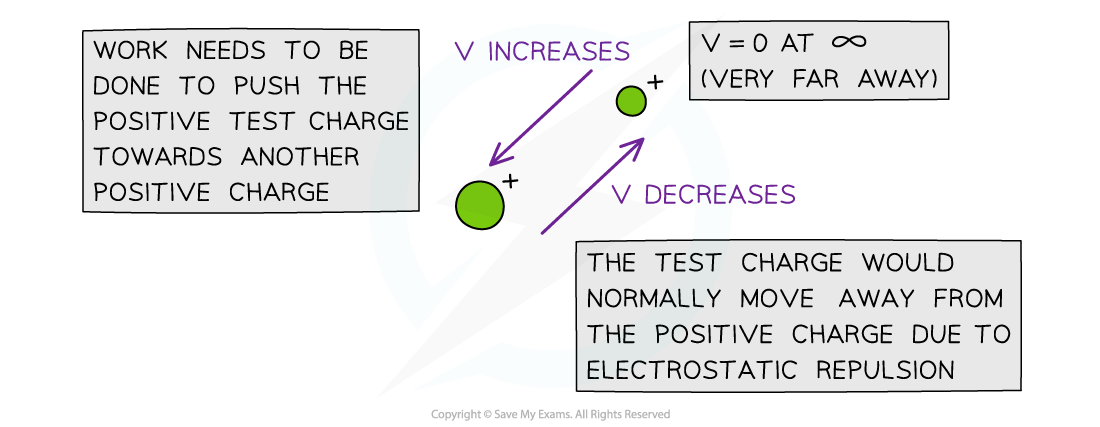
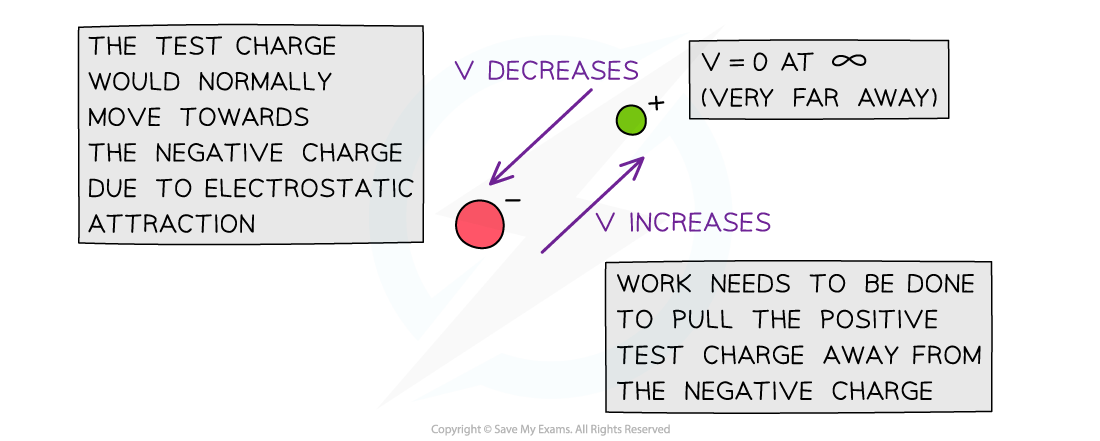
The electric potential V decreases in the direction the test charge would naturally move in due to repulsion or attraction

Electric Potential due to a Point Charge

• The electric potential in the radial field due to a point charge is defined as:

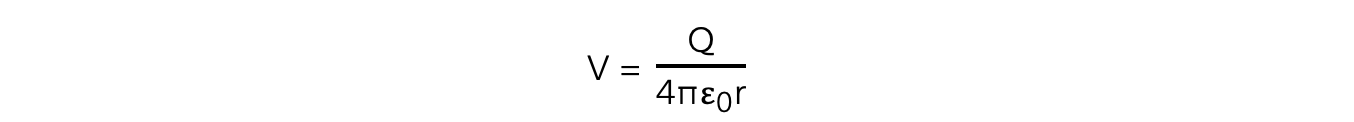
• Where:
  • V = the electric potential (V)
  • Q = the point charge producing the potential (C)
  • ε₀ = permittivity of free space (F m^-1)
  • r = distance from the centre of the point charge (m)

• This equation shows that for a positive test charge:
  • As the distance r from the charge Q decreases, the potential V increases (becomes more positive)
  • This is because more work has to be done on the positive test charge to overcome the repulsive force of Q

• For a negative test charge:
  • As the distance from the charge r decreases, the potential V decreases (becomes more negative)
  • This is because less work has to be done on the negative test charge since the attractive force becomes stronger the nearer it gets to Q

   

• Unlike the gravitational potential equation, the electric potential can be positive or negative, because Q can be positive or negative
• The electric potential varies according to 1 / r
  • Note, this is different to electric field strength, which varies according to 1 / r²

Step 1: Write the equation for electric potential

• • The electric potential is given by the equation:

Step 2: Write the transformed equation for a distance three times as large

• • The charge Q remains constant (due to the proton)
  • The potential V becomes V' 
  • The distance r becomes 3r
  • Hence the transformed equation becomes: 

Step 3: Write a conclusion

• • Therefore, when the distance from a charge Q gets three times larger, the value of the electric potential decreases by a factor 1/3, because the potential is inversely proportional to distance r