Electric Field between Parallel Plates (Edexcel International A Level Physics)

• The magnitude of the electric field strength in a uniform field between two charged parallel plates is defined as:

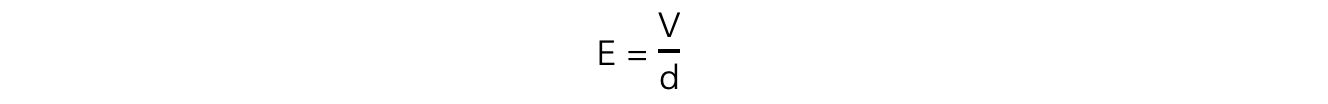
• Where:
  • E = electric field strength (V m^-1)
  • V = potential difference between the plates (V)
  • d = separation between the plates (m)

• The electric field strength is now defined by the units V m^–1 
  • Therefore, the units V m^–1 are equivalent to the units N C^–1

• The equation shows:
  • The greater the voltage (potential difference) between the plates, the stronger the field
  • The greater the separation between the plates, the weaker the field

• Remember this equation cannot be used to find the electric field strength around a point charge (since this would be a radial field)
• The direction of the electric field is from the plate connected to the positive terminal of the cell to the plate connected to the negative terminal

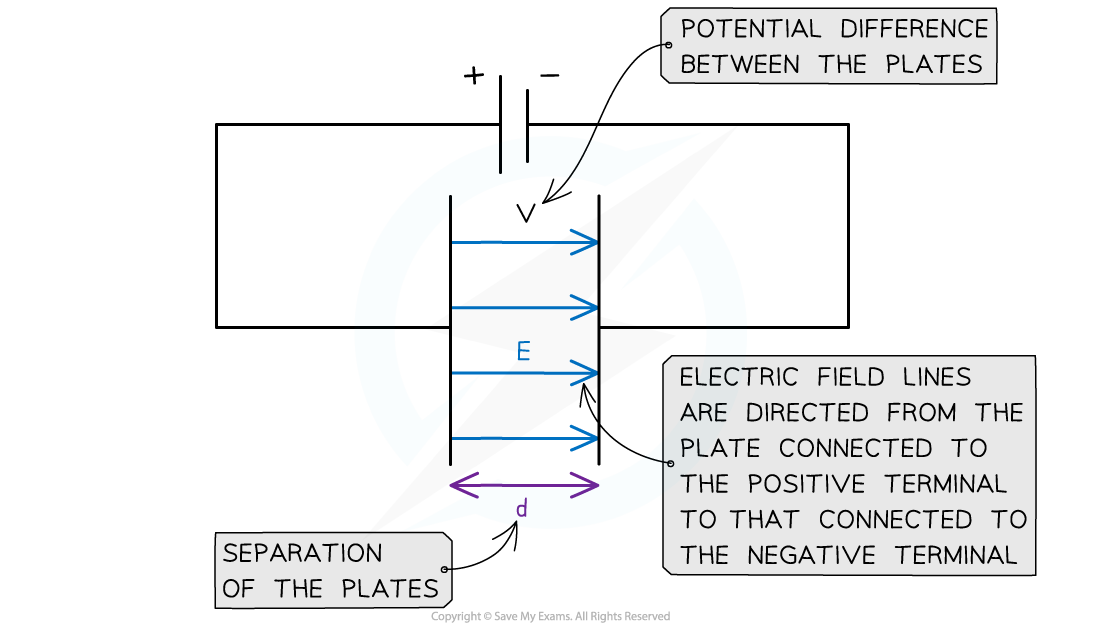
The E field strength between two charged parallel plates is the ratio of the potential difference and separation of the plates

• Note: if one of the parallel plates is earthed, it has a voltage of 0 V

Step 1: Write down the known values

• • Potential difference, V = 7.9 kV = 7.9 × 10³ V
  • Distance between plates, d = 3.5 cm = 3.5 × 10^-2 m
  • Charge, Q = 2.6 × 10^-15 C

Step 2: Calculate the electric field strength between the parallel plates

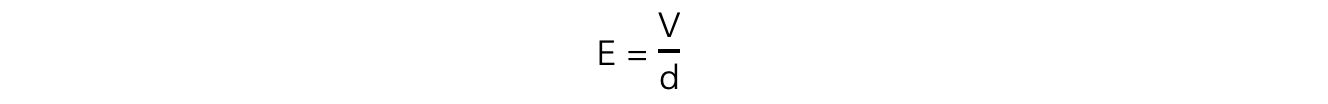
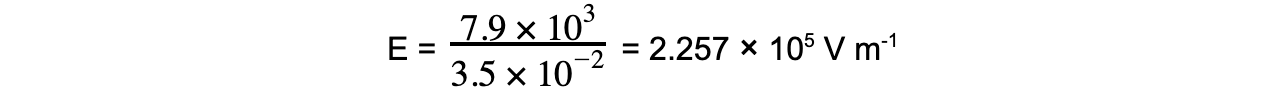
Step 3: Write out the equation for electric force on a charged particle

F = QE

Step 4: Substitute electric field strength and charge into electric force equation

F = QE = (2.6 × 10^-15) × (2.257 × 10⁵) = 5.87 × 10^-10 N = 5.9 × 10^-10 N (2 s.f.)