Electric Force between Two Charges (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Electric Force between Two Charges
All charged particles produce an electric field around them
This field exerts a force on any other charged particle within range
The electrostatic force between two charges is defined by Coulomb’s Law
Recall that the charge of a uniform spherical conductor can be considered as a point charge at its centre
Coulomb’s Law states that:
The electrostatic force between two point charges is proportional to the product of the charges and inversely proportional to the square of their separation
The force FE between two charges as expressed by Coulomb's Law is given by the equation:
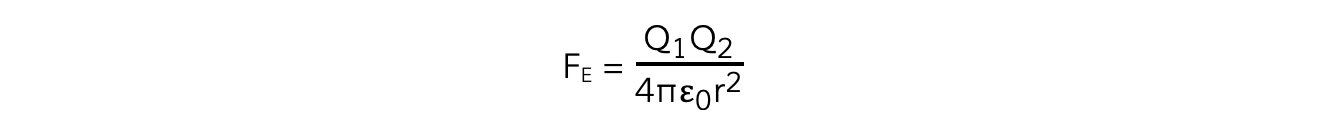

The electrostatic force between two charges is defined by Coulomb’s Law
Where:
FE = electrostatic force between two charges (N)
Q1 and Q2 = two point charges (C)
ε0 = permittivity of free space
r = distance between the centre of the charges (m)
The 1/r2 relation is called the inverse square law
This means that when the separation of two charges doubles, the electrostatic force between them reduces to (½)2 = ¼ of its original size
ε0 is a physical constant used to show the capability of a vacuum to permit electric fields
If Q1 and Q2 are oppositely charged, then the electrostatic force FE is negative
This can be interpreted as an attractive force between Q1 and Q2
If Q1 and Q2 are the same charge, then the electrostatic force FE is positive
This can be interpreted as a repulsive force between Q1 and Q2
Worked Example
An alpha particle is situated 2.0 mm away from a gold nucleus in a vacuum. Assuming they are point charges, calculate the magnitude of the force acting on each of the charges.
Atomic number of helium = 2
Atomic number of gold = 79
Charge of an electron = 1.60 × 10-19 C
Answer:
Step 1: Write down the known quantities
Distance, r = 2.0 mm = 2.0 × 10-3 m
The charge of one proton = +1.60 × 10-19 C
An alpha particle (helium nucleus) has 2 protons
Charge of alpha particle, Q1 = 2 × 1.60 × 10-19 = +3.2 × 10-19 C
The gold nucleus has 79 protons
Charge of gold nucleus, Q2 = 79 × 1.60 × 10-19 = +1.264 × 10-17 C
Step 2: The electrostatic force between two point charges is given by Coulomb’s Law
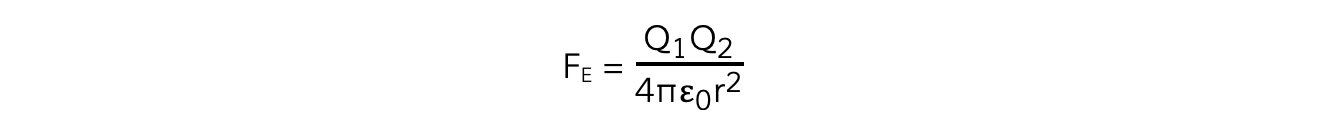
Step 3: Substitute values into Coulomb's Law
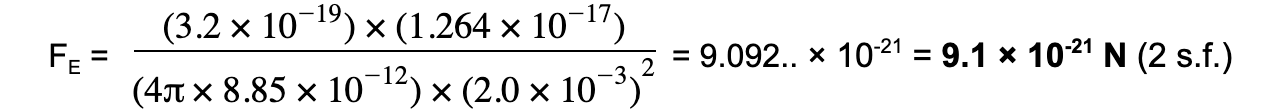
Examiner Tips and Tricks
Remember to always square the distance, r between the charges!
Always look out for unit prefixes when substituting values into an equation. Check whether the charge has been converted into C instead of nC or µC, or the distance in mm to m to get a force F of newtons, N.

Unlock more, it's free!
Did this page help you?