Radians
- A radian (rad) is defined as:
The angle subtended at the centre of a circle by an arc equal in length to the radius of the circle
- Radians are used whenever describing the angular displacement of objects in circular motion
- Angular displacement can be calculated using the equation:
- Where:
- Δθ = angular displacement, or angle of rotation (radians)
- s = length of the arc, or the distance travelled around the circle (m)
- r = radius of the circle (m)
- Radians are commonly written in terms of π
- The angle in radians for a complete circle (360o) is equal to:
Radian Conversions
- If an angle of 360o = 2π radians, then 1 radian in degrees is equal to:
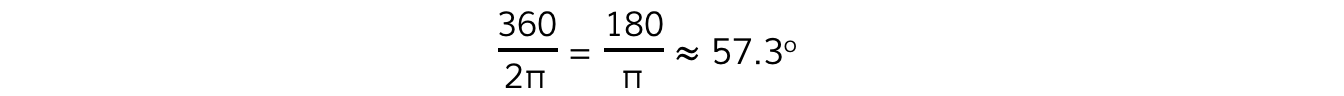
- Use the following equation to convert from degrees to radians:
Table of common degrees to radians conversions
Worked example
Convert the following angular displacement into degrees:
Examiner Tip
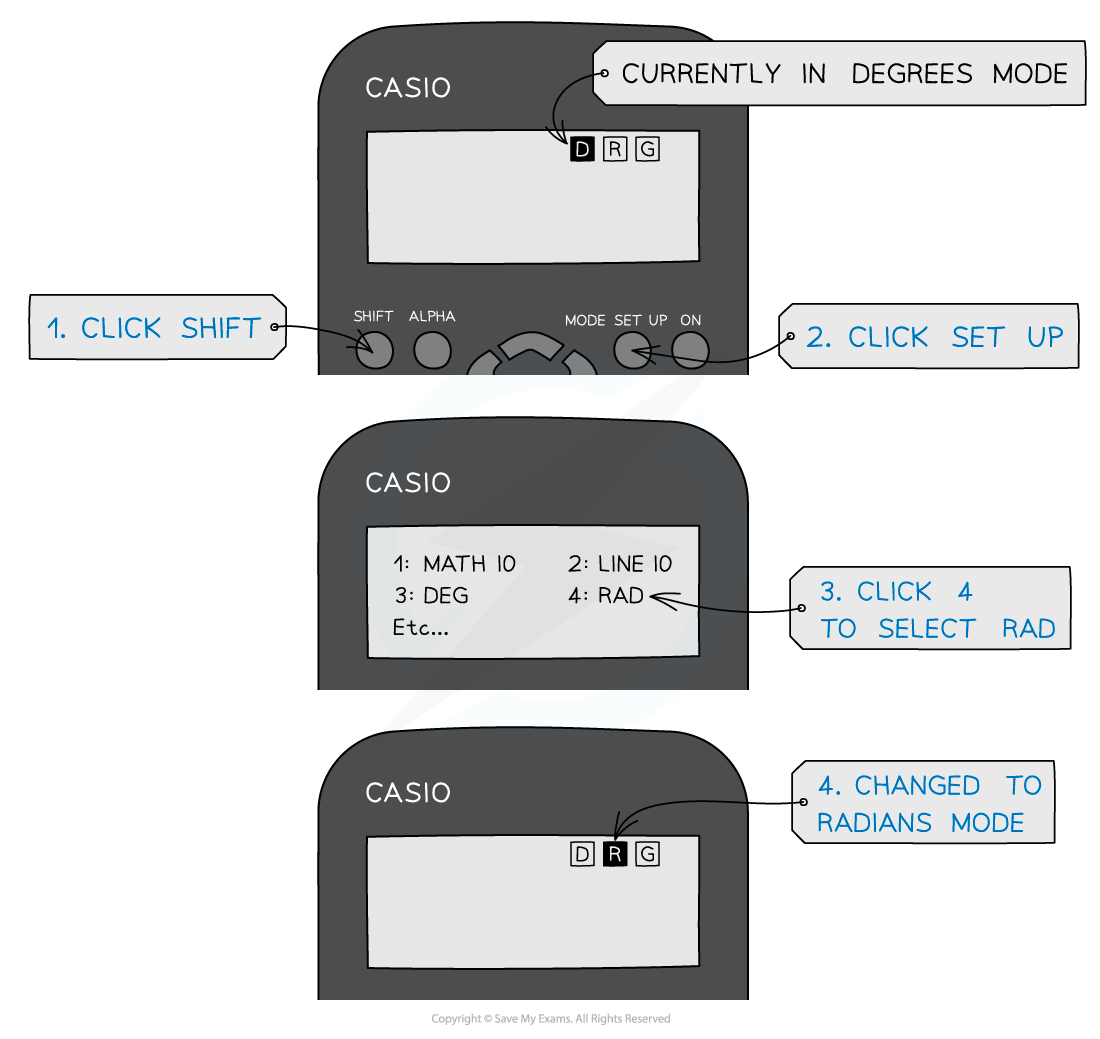
- You will notice your calculator has a degree (Deg) and radians (Rad) mode
- This is shown by the “D” or “R” highlighted at the top of the screen
- Remember to make sure it’s in the right mode when using trigonometric functions (sin, cos, tan) depending on whether the answer is required in degrees or radians
- It is extremely common for students to get the wrong answer (and lose marks) because their calculator is in the wrong mode when using trigonometric functions - make sure this doesn’t happen to you!
