Identifying Graphical Relationships (Edexcel International A Level Physics)

• Graphs are used to visualise the relationship between two sets of data from two different variables
• Common relationships are:
  • Directly proportional
  • Inversely proportional
• A direct proportionality relationship is where as one amount increases, another amount increases at the same rate
  
  • This is represented by a straight-line graph with a positive gradient
• For two variables, y and x this looks like:

y ∝ x

• An inverse proportionality relationship is where as one amount increases, another amount decreases at the same rate
  • This is represented by a curved graph with a decreasing gradient
• For two variables, y and x this looks like:

y ∝ 

Sketched graphs show relationships between variables

• In the first sketch graph, above you can see that the relationship is a straight line going through the origin
  • This means as you double one variable the other variable also doubles so we say the independent variable is directly proportional to the dependent variable
• The second sketched graph shows a shallow curve
  • This is the characteristic shape when two variables have an inversely proportional relationship
• The third sketched graph shows a straight horizontal line,
  • This means as the independent variable (x-axis) increases the dependent variable does not change or is constant

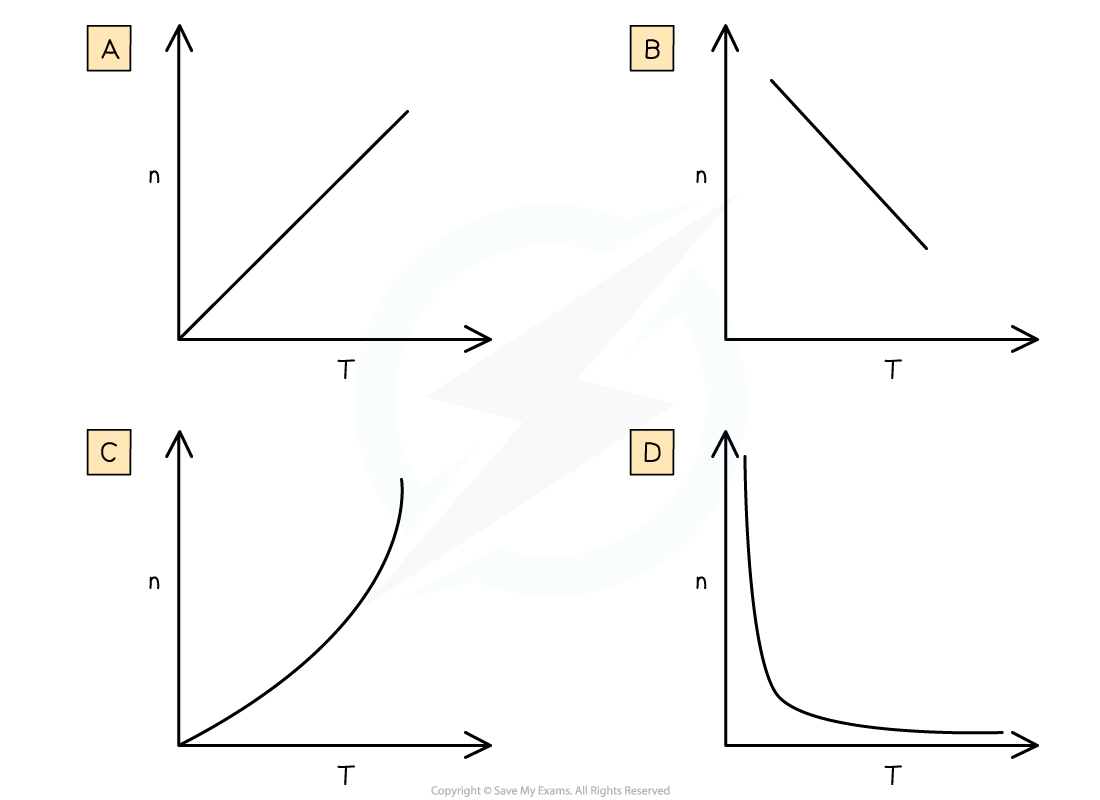
Answer: D

• The Ideal Gas Equation is PV= nRT
  • If P, V and R are constant then  = nT = a constant
• n must be inversely proportional to T
  • This is graph D