Uncertainty & Systematic Errors (Edexcel International A Level Physics)

Predicting Uncertainty & Systematic Errors

Predicting Uncertainties

• The uncertainty is an estimate of the difference between a measurement reading and the true value

  • In other words, it is the interval within which the true value can be considered to lie with a given level of confidence or probability

  • Any measurement will have some uncertainty about the result, this will come from variation in the data obtained and be subject to systematic or random effects

• In reality, it is impossible to obtain the true value of any quantity as there will always be a degree of uncertainty

  • This can be seen when you repeat a measurement and you often get different results

• Uncertainties are not the same as errors

• An error is the difference between the measurement result and the true value if a true value is thought to exist

  • This is not a mistake in the measurement

  • The error can be due to both systematic and random effects and an error of unknown size is a source of uncertainty.

  • They can be thought of as issues with equipment or methodology that cause a reading to be different from the true value 

• The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate

  • For example, if the true value of the mass of a box is 950 g, but a systematic error with a balance gives an actual reading of 952 g, the uncertainty is ±2 g

• The most common ways to reduce uncertainties are:

  • Take repeat readings (about 3 – 5) and calculate the mean of a value

  • For a wire, measure the diameter in different places, to make sure it's fully uniform

  • Use the appropriate piece of apparatus for the measurement e.g., do not use a ruler for a very small distance of a few mm, a micrometer or vernier scale would be better for this

Systematic errors

• Systematic errors arise from the use of faulty instruments or from flaws in the experimental method

• This type of error is repeated consistently every time the instrument is used or the method is followed, which affects the accuracy of all readings obtained

• Systematic errors can clearly be seen on graphs

  • If the line of best fit of a straight-line graph is expected to go through the origin (0,0) but the results collected actually pass through the y or x axis instead, then all the points are offset by the same amount

  • The amount they are offset by is the amount of systematic errors

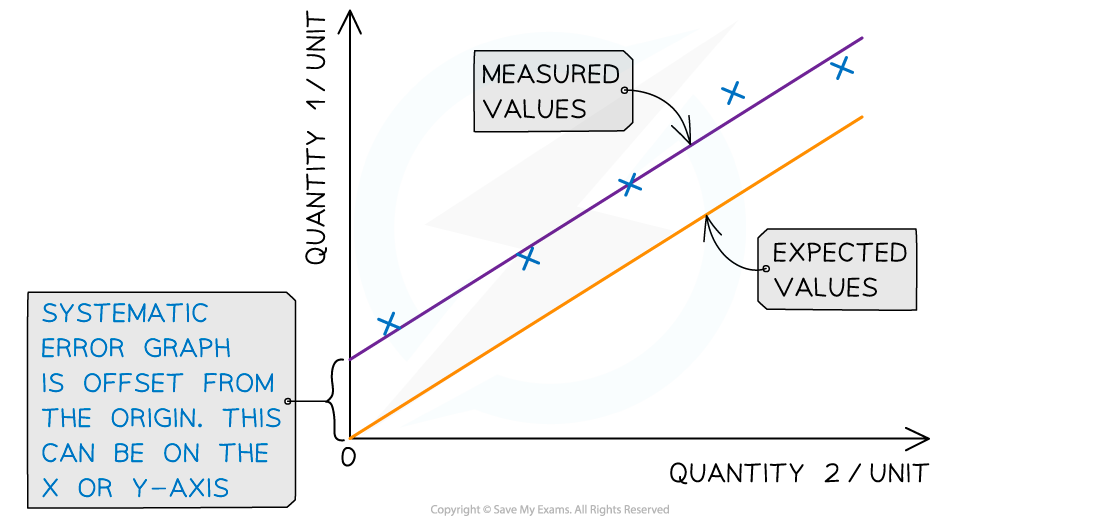
Systematic errors on graphs are shown by the offset of the line from the origin

• To reduce systematic errors:

  • Instruments should be recalibrated, or different instruments should be used

  • Corrections or adjustments should be made to the technique

• An example of a systematic error is a zero error

• A common method for measuring small distances, such as the fringe spacing on an interference pattern, is measuring a larger distance (multiple fringe spacings) and divide by the number of fringe spacings

  • A fringe spacing is a very small measurement and it is often difficult to see the middle of each bright fringe (the maxima can be broad)

• The same can be done for oscillations

  • Measuring the time for 10 oscillations, then dividing by 10 is more accurate than just timing 1 oscillation

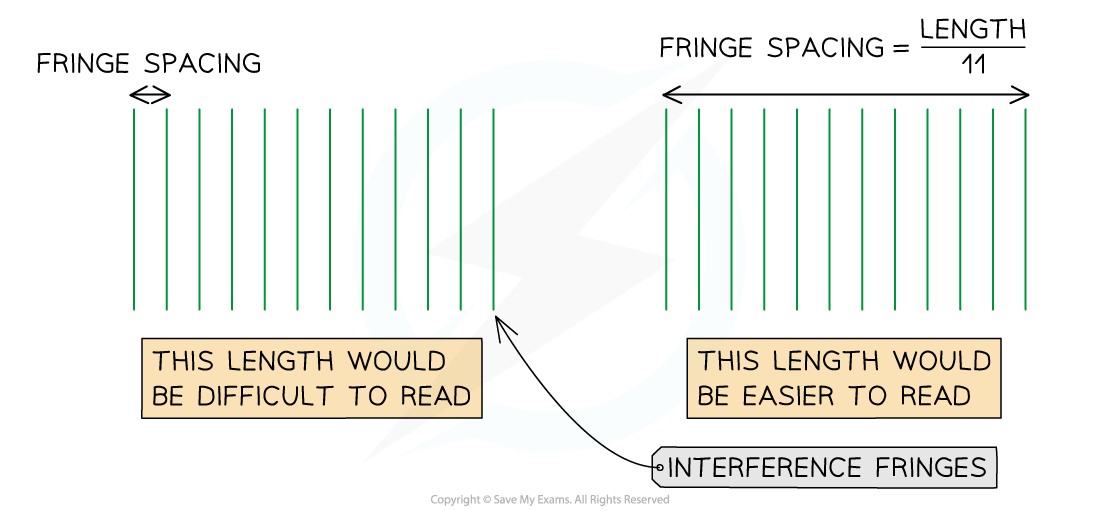
Measuring the distance between multiple fringes reduces the uncertainty in the fringe spacing