Atomic Line Spectra (Edexcel International A Level Physics)

Atomic Line Spectra

• An emission line spectrum is produced when:

  An excited electron in an atom moves from a higher to a lower energy level and emits a photon with an energy corresponding to the difference between these energy levels

• Each element produces a unique emission line spectrum due to its unique set of energy levels

  • Hot gases produce emission line spectra, such as stars

• When the atoms of a gas are excited, electrons gain energy and move to higher energy levels

When an electron moves from a higher energy level to a lower energy level, a photon is released

• Electrons cannot stay in a continuous state of excitation, so they will move back to lower energy levels through de-excitation

  • During de-excitation, energy must be conserved, so transitions result in an emission of photons with discrete frequencies (or wavelengths) specific to that element

  • Since there are many possible electron transitions for each atom, there are many different radiated wavelengths

  • This creates a line spectrum consisting of a series of bright lines against a dark background

  • An emission line spectrum acts as a fingerprint of the element

An example of the emission line spectrum of hydrogen

• Each line of the emission spectrum corresponds to a different energy level transition within the atom

  • Electrons can transition between energy levels absorbing or emitting a discrete amount of energy

  • An excited electron can transition down to the next energy level or move to a further level closer to the ground state

• For example, if an atom has six energy levels:

  • At low temperatures, most electrons will occupy the ground state n = 1

  • At high temperatures, electrons may be excited to the most excited state n = 6

Energy and frequency of a photon are directly proportional

• The energy of a photon is given by the equation:

E = hf

• Using energy can be written as:

E = 

• Where:

  • E = energy of the photon (J)

  • h = Planck's constant(J s)

  • c = speed of light (m s^-1)

  • f = frequency (Hz)

  • λ = wavelength (m)

• The energy required to move from one energy level to another is given by the difference of energy between the two energy levels:

ΔE = E₁ – E₂

• Where:

  • E₁ = energy associated with the level that the electron has left (eV)

  • E₂ = energy associated with the level that the electron moves to (eV)

• The difference of energy corresponds to the energy of the absorbed (or emitted) photon:

ΔE = E₁ – E₂ = hf = 

• For each transition, a photon will be emitted with a specific wavelength

• In the case of hydrogen, all wavelengths are in the visible range:

  • From n = 6 to n = 2 - violet

  • From n = 5 to n = 2 - blue

  • From n = 4 to n = 2 - light blue

  • From n = 3 to n = 2 - red

If the emitted photons are in the visible range, wavelengths can be represented as lines of the respective colour against a black background

• Emitted photons can have a range of wavelengths spanning the whole electromagnetic spectrum

  • The wavelength is inversely proportional to the energy level transition associated with the emitted photon

• For example, the transitions for hydrogen will be as follows:

  • To n = 1 (ground level) – ultraviolet, highest energy, high frequency, short wavelength

  • To n = 2 – visible light, violet is the highest energy, red is the lowest energy

  • To n = 3 – infrared light, lowest energy, low frequency, longest wavelength

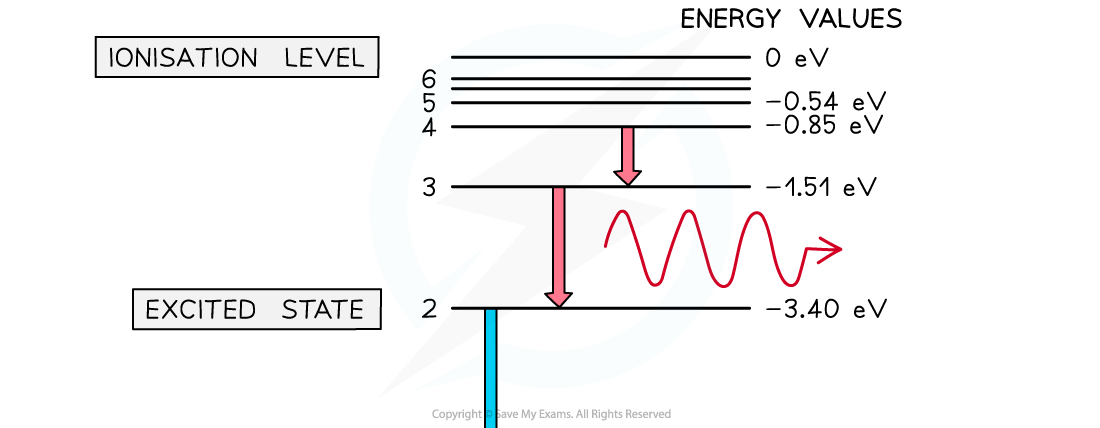
The larger the energy transition, the longer the wavelength of the emitted photon