Calculating Current & Drift Velocity (Edexcel International A Level Physics)

Calculating Current & Drift Velocity

Drift Velocity

• In a conductor, the current is due to the movement of charge carriers

  • The charge carriers can be negative or positive

  • However current is always taken to be in the same direction

• Drift velocity is the average velocity of the charge carriers travelling through the conductor

• In conductors, the charge carrier is usually free electrons

  • Free electrons only travel small distances before colliding with a metal ion

  • Therefore they have a relatively slow drift velocity of ∼ 10⁻³ m s⁻¹

• In the diagram below, the current in each conductor is from right to left

  • In diagram A (positive charge carriers), the drift velocity is in the same direction as the current

  • In diagram B (negative charge carriers), the drift velocity is in the opposite direction to the current

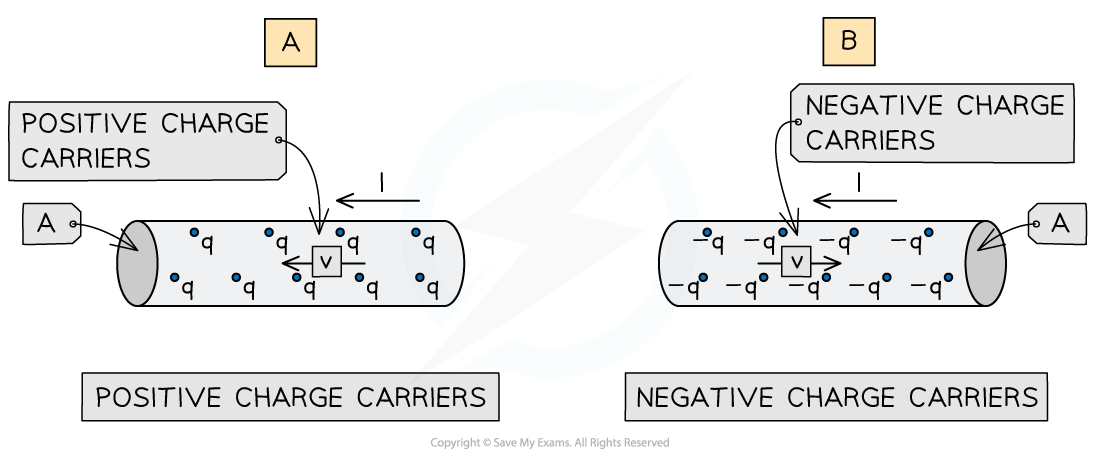
Conduction in a current-carrying conductor

• The density n represents the number of free charge carriers (electrons) per unit volume

  • Conductors, such as metals, have a high value of n

  • Insulators, such as plastics, have a low value of n

• Since the density of charge carriers is so large in conductors, the flow of current flow appears to happen instantaneously

The Transport Equation

• The current can be expressed in the transport equation:

• Where:

  • I = current (A)

  • n = number density (m⁻³)

  • q = the charge of the charge carrier (C)

  • v = drift velocity (m s⁻¹)

  • A = cross sectional area of the wire (m²), calculated using A = πr²

• The same equation is used whether the charge carriers are positive or negative

  • A negative value for v will indicate current in the opposite direction to the charge carriers

• The transport equation shows that v is inversely proportional to n

  • Since the more charge carriers available per unit volume the more the density will slow down their speed through the conductor

• The transport equation also shows that I is directly proportional to n 

  • Greater n means a greater charge is flowing and therefore a larger current I

• When the value of n is lower, the charge carriers must travel faster to carry the same current

The Large Range of Material Resistivities

Resistivity

• The transport equation tells us that current, I ∝ number of charge carriers, n

  • Therefore, the larger the number of charge carriers, the greater the current will be for the same applied voltage

  • This is because resistivity has decreased with more charge carriers available

• Different materials have different numbers of charge carriers

• Insulators have few charge carriers:

  • They have such a high resistivity that virtually no current will flow through them

  • A perfect insulator would have no charge carriers, n = 0 

  • A perfect insulator would have a current of zero regardless of the voltage applied

• Conductors have a large number of charge carriers

  • Metals are good conductors because they have free electrons

  • Free electrons are the atoms from the outer shell of each atom

  • Therefore there are lots of charge carriers per unit volume

  • This means resistivity is low

• Semiconductors have a small number of free electrons

  • There are fewer delocalised electrons in a semiconductor than in a metal 

  • There are a greater number of free electrons at a higher temperature

  • Resistivity changes in a semiconductor, due to the variation with temperature in free electrons which are available as charge carriers 

  • Silicon is an example of a semiconductor

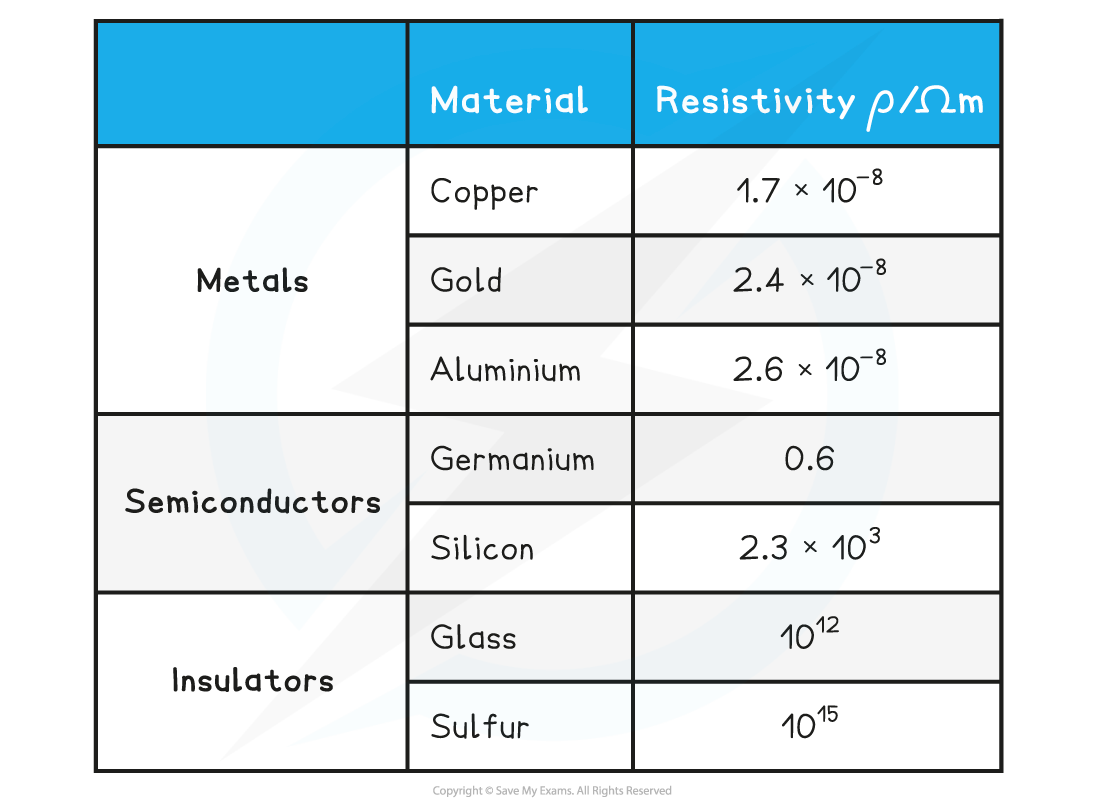
The resistivity of some materials at room temperature