Equation for the Intensity of Radiation
- Progressive waves transfer energy
- The amount of energy passing through a unit area per unit time is the intensity of the wave
- Therefore, the intensity is defined as power per unit area

Intensity is equal to the power per unit area
- The area the wave passes through is perpendicular to the direction of its velocity
- The intensity of a progressive wave is also proportional to its amplitude squared and frequency squared
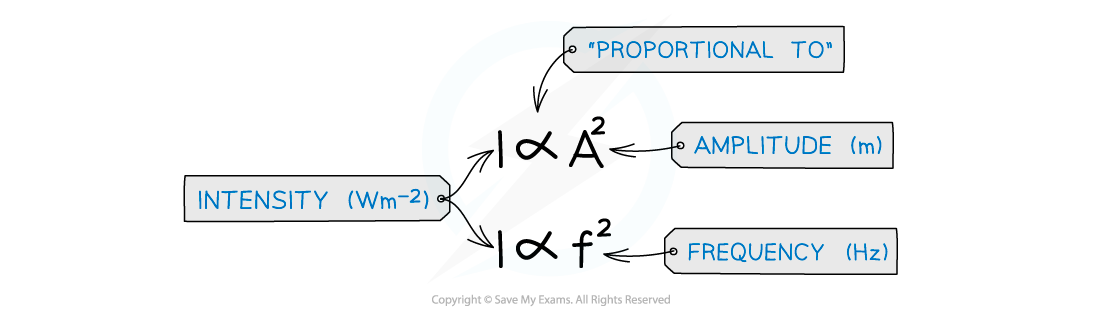
Intensity is proportional to the amplitude2 and frequency2
- This means, if the frequency or the amplitude is doubled, the intensity increases by a factor of 4 (22)
Spherical Waves
- A spherical wave is a wave from a point source that spreads out equally in all directions
- The area the wave passes through is the surface area of a sphere: 4πr2
- As the wave travels further from the source, the energy it carries passes through increasingly larger areas as shown in the diagram below:

Intensity is proportional to the amplitude squared
- Assuming there’s no absorption of the wave energy, the intensity I decreases with increasing distance from the source
- Note the intensity is proportional to 1/r2
- This means when the source is twice as far away, the intensity is 4 times less
- The 1/r2 relationship is known in physics as the inverse square law
Worked example
The intensity of a progressive wave is proportional to the square of the amplitude of the wave. It is also proportional to the square of the frequency. The variation with time t of displacement x of particles when two progressive waves Q and P pass separately through a medium are shown on the graphs The intensity of wave Q is I0. What is the intensity of wave P?
The intensity of wave Q is I0. What is the intensity of wave P?


Examiner Tip
The key concept with intensity is that it has an inverse square relationship with distance (not a linear one). This means the energy of a wave decreases very rapidly with increasing distance

