Wave Speed on a Stretched Spring (Edexcel International A Level Physics)

• The speed of a wave travelling along a string with two fixed ends is given by:

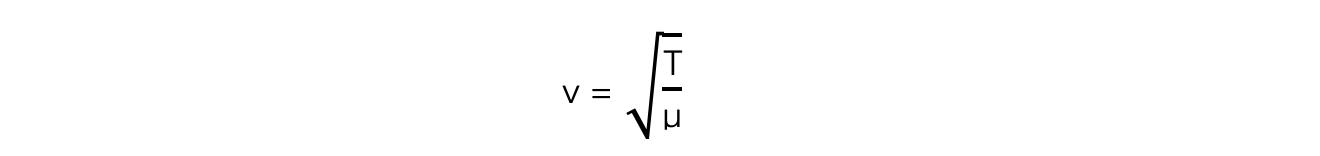
• Where:
  • T = tension in the string (N)
  • μ = mass per unit length of the string (kg m^–1)

 

• At the fundamental frequency, f₀ of a stationary wave of length L, the wavelength, λ = 2L
• Therefore, according to the wave equation, the speed of the stationary wave is:

v = fλ = f × 2L

• Combining these two equations leads to the equation for the fundamental frequency (sometimes referred to as the first harmonic):

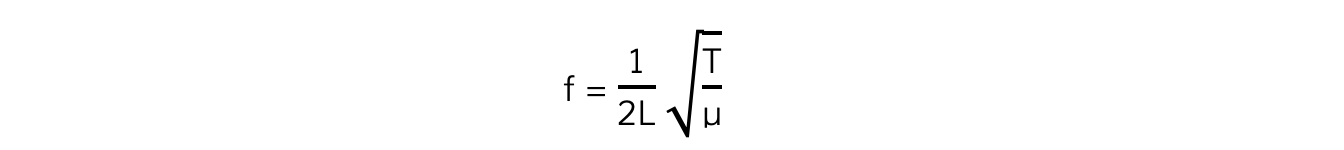
• Where:
  • f = frequency (Hz)
  • L = the length of the string (m)
  • T = the tension in the string (N)
  • µ = mass per unit length (kg m^-1)

• Mass per unit length, µ can be calculated by dividing the mass of the string by the length of the string

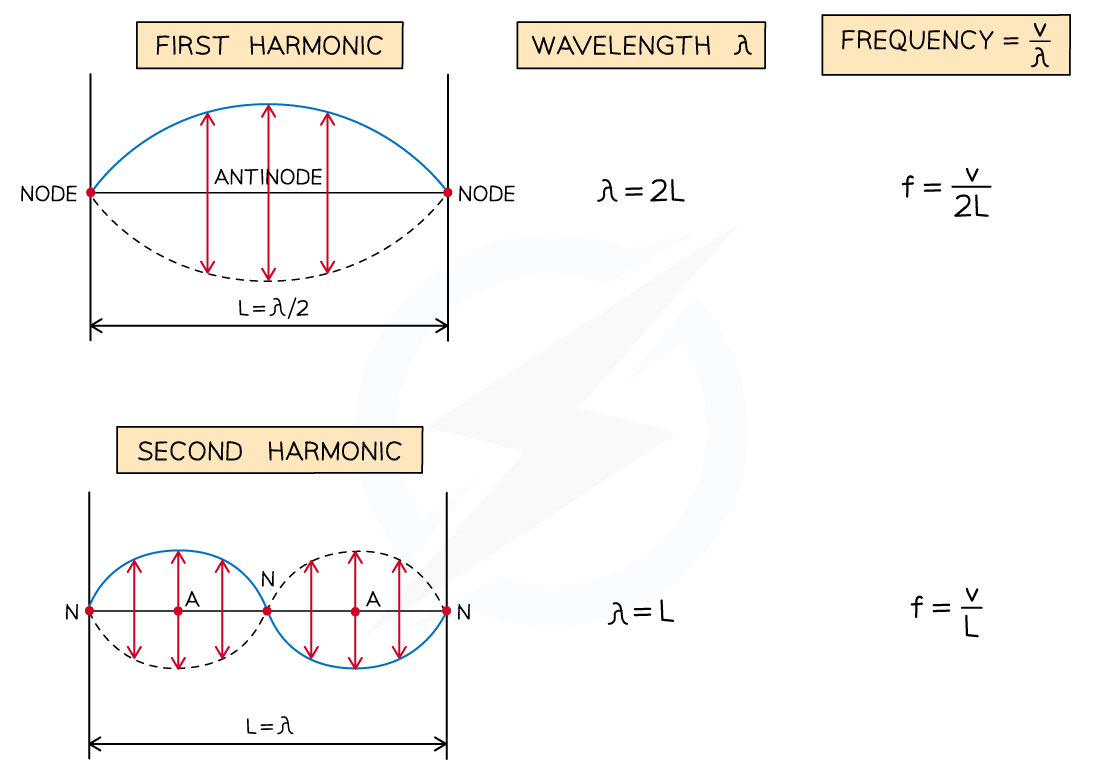
Diagram showing the first three modes of vibration of a stretched string with corresponding frequencies

Part (a)

Step 1: Write the known quantities in S.I. units

• • Tension, T = 65 N
  • Mass, m = 3.2 g = 3.2 × 10⁻³ kg
  • Length of string, L = 90 cm = 0.90 m

    • Mass per unit length, μ =  = 3.56 × 10⁻³ kg m⁻¹

Step 2: Write the equation for speed on a string and calculate

• • v = fλ = f × 2L AND f = 
  • So, v =

= 135

Step 3: Write the answer to the correct significant figures and include units

• • The speed of the wave on the string, v = 140 m s⁻¹

Part (b)

Step 1: Write the known quantities in S.I. units

• • Tension, T = 65 N
  • Length of string under tension, L = 75 cm = 0.75 m
  • Mass per unit length, μ = 3.56 × 10⁻³ kg m⁻¹ (from part (a))

Step 2: Identify the length of one wavelength at the fundamental frequency, f₀

Step 3: Write the equation for fundamental frequency and calculate

= 90.1

Step 3: Write the answer to the correct significant figures and include units

• • The fundamental frequency, f₀ = 90 Hz