E.M.F. vs. Terminal Potential Difference (Edexcel International A Level Physics)

E.M.F. vs. Terminal Potential Difference

Terminal Potential Difference

• The terminal potential difference (p.d.) is the potential difference across the terminals of a cell

  • If there was no internal resistance, the terminal p.d. would be equal to the e.m.f.

  • If a cell has internal resistance, the terminal p.d. is always lower than the e.m.f.

  • If you have a load resistor R across the cell's terminals, then the terminal p.d. is also the potential difference across the load resistor

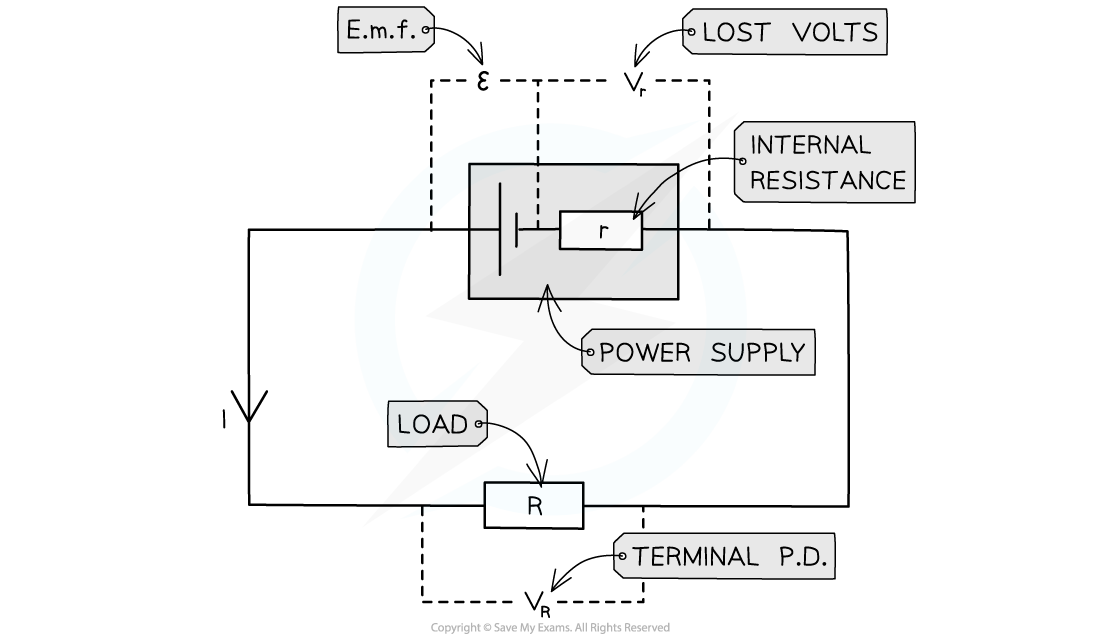
Circuit showing the e.m.f. and internal resistance of a power supply

• Where:

  • Resistor R is the ‘load resistor’

  • r is the internal resistance

  • ε is the e.m.f.

  • V_r is the lost volts

  • V_R is the p.d across the load resistor, which is the same as the terminal p.d.

• Terminal potential difference is the voltage available to the rest of the circuit

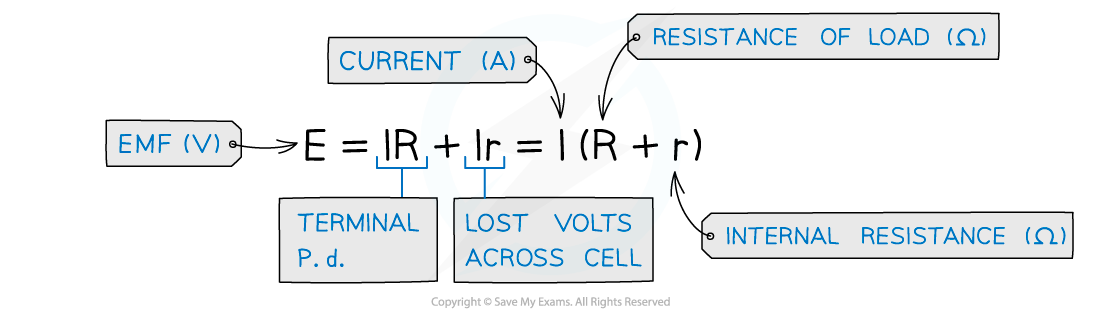
V_R = I × R  ( from Ohm’s law)

• Where:

  • R = load resistance (Ω)

  • I = current in the circuit (A)

  • V_R = Terminal p.d. (V)

• When a load resistor is connected, current flows through the cell and a potential difference develops across the internal resistance.

  • This voltage is not available to the rest of the circuit so is called the ‘lost volts’

• V_r is the lost volts

  • This is the voltage lost in the cell due to internal resistance

V_r = I × r (from Ohm’s law)

• Where:

  • r = internal resistance (Ω)

  • I = current in the circuit (A)

  • V_r = Lost volts (V)

• The e.m.f. is the sum of the terminal p.d. and the lost volts:

The Difference Between Potential Difference and E.M.F

• The difference between potential difference and e.m.f is the type of energy transfer per unit charge

• When charge passes through a resistor, for example, its electrical energy is converted to heat in the resistor

  • The resistor, therefore, has a potential difference across it

• Potential difference describes the loss of energy from charges

  • Ie. when electrical energy is transferred to other forms of energy in a component

• E.m.f. describes the transfer of energy from the power supply to electrical charges within the circuit