Revision NotesExam QuestionsPast Papers
International A LevelPhysicsEdexcelRevision Notes1. Mechanics & MaterialsWork, Energy & PowerEfficiency

Efficiency (Edexcel International A Level Physics)

Revision Note

Lindsay Gilmour

Last updated

Efficiency

  • The efficiency of a system is a measure of how well energy is transferred in a system

  • Efficiency is defined as:

    The ratio of the useful power or energy transfer output from a system to its total power or energy transfer input

  • If a system has high efficiency, this means most of the energy transferred is useful

  • If a system has low efficiency, this means most of the energy transferred is wasted

  • Determining which type of energy is useful or wasted depends on the system

    • When electrical energy is converted to light in a lightbulb, the light energy is useful and the heat energy produced is wasted

    • When electrical energy is converted to heat for a heater, the heat energy is useful and the sound energy produced is wasted

  • Efficiency can be given as a ratio (between 0 and 1) or a percentage (between 0 and 100%)

  • Since efficiency is a ratio, it has no units

  • Calculate energy efficiency and power efficiency in the same way, using one of the following equations;

Efficiency equation, downloadable AS & A Level Physics revision notes

  • The energy can be of any form e.g. gravitational potential energy, kinetic energy

Efficiency equation 2, downloadable AS & A Level Physics revision notes

  • Where power is defined as the energy transferred per unit of time

Worked Example

An electric motor has an efficiency of 35 %. It lifts a 7.2 kg load through a height of 5 m in 3 s.

Calculate the power of the motor.

Answer:

Step 1: Write down the efficiency equation 

Efficiency equation

Step 2: Rearrange for the power input  

Worked Example Power Input Equation

Step 3: Calculate the power output

  • The power output is equal to energy ÷ time

  • The electric motor transferred electric energy into gravitational potential energy to lift the load

Gravitational potential energy = mgh = 7.2 × 9.81 × 5 = 353.16 J

Power = 353.16 ÷ 3 = 117.72 W

Step 4: Substitute values into power input equation 

Power Input Worked Example Answer

Worked Example

The diagram shows a pump called a hydraulic ram.

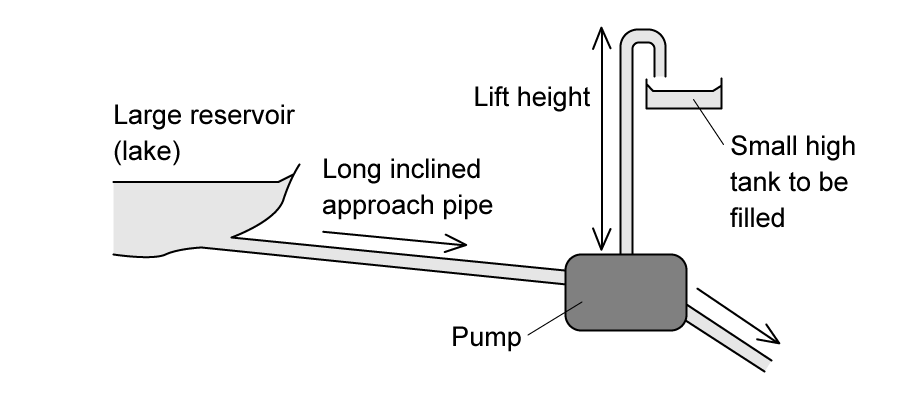
In one such pump, the long approach pipe holds 700 kg of water. A valve shuts when the speed of this water reaches 3.5 m s-1 and the kinetic energy of this water is used to lift a small quantity of water by height of 12m.

The efficiency of the pump is 20%.

Determine the mass of water which could be lifted 12 m

Answer:

Step 1: Identify the energy conversions and write them in an equation

  • The kinetic energy of the moving water is converted to gravitational potential energy as it is lifted

  • The equation should be that;

   i n i t i a l space E subscript k equals f i n a l space E subscript g r a v end subscript → 1 half m v squared equals m g capital delta h

Step 2: Include the efficiency in the equation

  • Efficiency = 20% meaning 20% of the kinetic energy is converted;

0.2 space cross times space 1 half m v squared equals m g capital delta h

Step 3: Substitute in the values and calculate

0.2 space cross times space 1 half space cross times space 700 space cross times space left parenthesis 3.5 squared right parenthesis space equals space m space cross times space 9.81 space cross times space 12

857.5 space equals space 117.72 space m

m = 7.284

Step 4: Write the answer with the correct significant figures and units

  • Mass of water lifted, m = 7.3 kg (2 s.f.)

Examiner Tips and Tricks

In efficiency calculations decide before starting where the energy is lost from the system.

In the example above, the pump is what converts the water’s kinetic energy into gravitational potential energy, and it is the pump whose efficiency we are given. That means the losses are from the kinetic energy.

Don't just calculate then deduct the efficiency at the end - this can lead to lots of work for no marks. Which isn't very efficient! 

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:PowerNext:Density
    Lindsay Gilmour

    Author: Lindsay Gilmour

    Expertise: Physics

    Lindsay graduated with First Class Honours from the University of Greenwich and earned her Science Communication MSc at Imperial College London. Now with many years’ experience as a Head of Physics and Examiner for A Level and IGCSE Physics (and Biology!), her love of communicating, educating and Physics has brought her to Save My Exams where she hopes to help as many students as possible on their next steps.