The Principle of Conservation of Energy (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
The Principle of Conservation of Energy
The principle of conservation of energy is a law of Physics which always applies to a closed system

To apply conservation of energy, heat losses are usually ignored during the calculation stage
In reality there are always some energy losses from the system
These should be mentioned when comparing calculated, ideal values to real-life situations
Conservation of energy is often applied in questions about exchanges between kinetic energy and gravitational energy
Common examples include:
A swinging pendulum
Objects in free fall
Sports such as skiing or skydiving where gravity is causing motion and few drag forces apply
The gravitational potential energy stored initially is transferred to kinetic energy, or vice versa
This allows either;
Final velocity to be found from the distance the object moved, or
Height of a drop from the final velocity
Worked Example
The diagram below shows a skier on a slope descending 750 m at an angle of 25° to the horizontal.
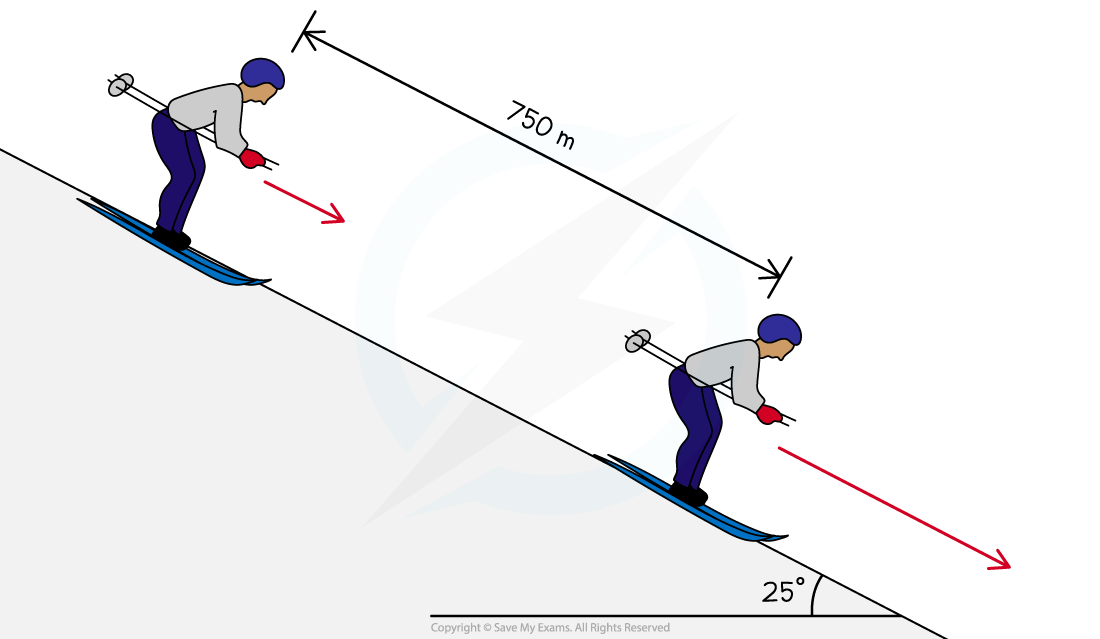
Calculate the final speed of the skier, assuming that he starts from rest and 15% of his initial gravitational potential energy is not transferred to kinetic energy.
Answer:
Step 1: Write down the known quantities
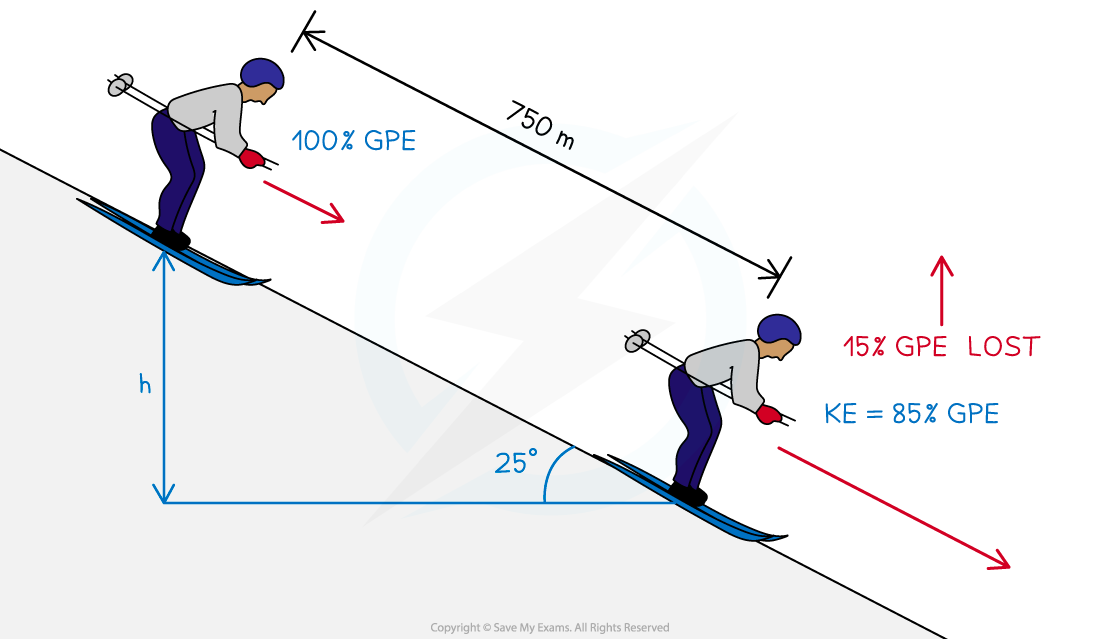
Vertical height, h = 750 sin 25°
Ek = 0.85 Ep
Step 2: Equate the equations for Ek and Egrav
Ek = 0.85 Egrav
½ mv2 = 0.85 × mgh
Step 3: Rearrange for final speed, v
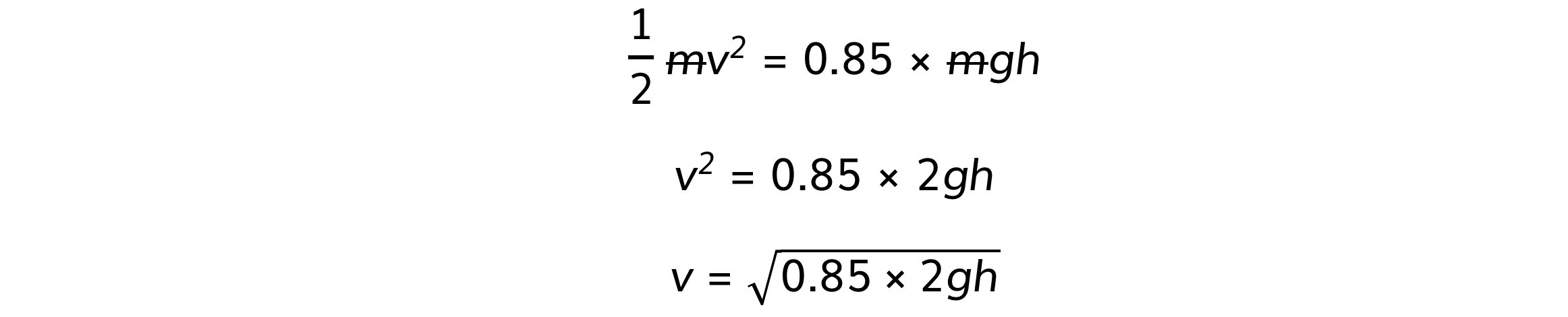
Step 4: Calculate the final speed, v

Examiner Tips and Tricks
Gravitational energy:
This equation only works for objects close to the Earth’s surface where we can consider the gravitational field to be uniform.
Kinetic energy:
When using the kinetic energy equation, note that only the speed is squared, not the mass or the ½.
If a question asks about the ‘loss of kinetic energy’, remember not to include a negative sign since energy is a scalar quantity.

Unlock more, it's free!
Did this page help you?