Hooke's Law (Edexcel International A Level Physics)

• When a force F is added to the bottom of a vertical metal wire of length L, the wire stretches
• A material obeys Hooke’s Law if:

The extension of the material is directly proportional to the applied force (load) up to the limit of proportionality

• This linear relationship is represented by the Hooke’s law equation:

ΔF = kΔx

• Where:
  • F = applied force (N)
  • k = spring constant (N m^–1)
  • Δx = extension (m)

• The spring constant is a property of the material being stretched and measures the stiffness of a material
  • The larger the spring constant, the stiffer the material

• Hooke's Law applies to both extensions and compressions:
  • The extension of an object is determined by how much it has increased in length
  • The compression of an object is determined by how much it has decreased in length

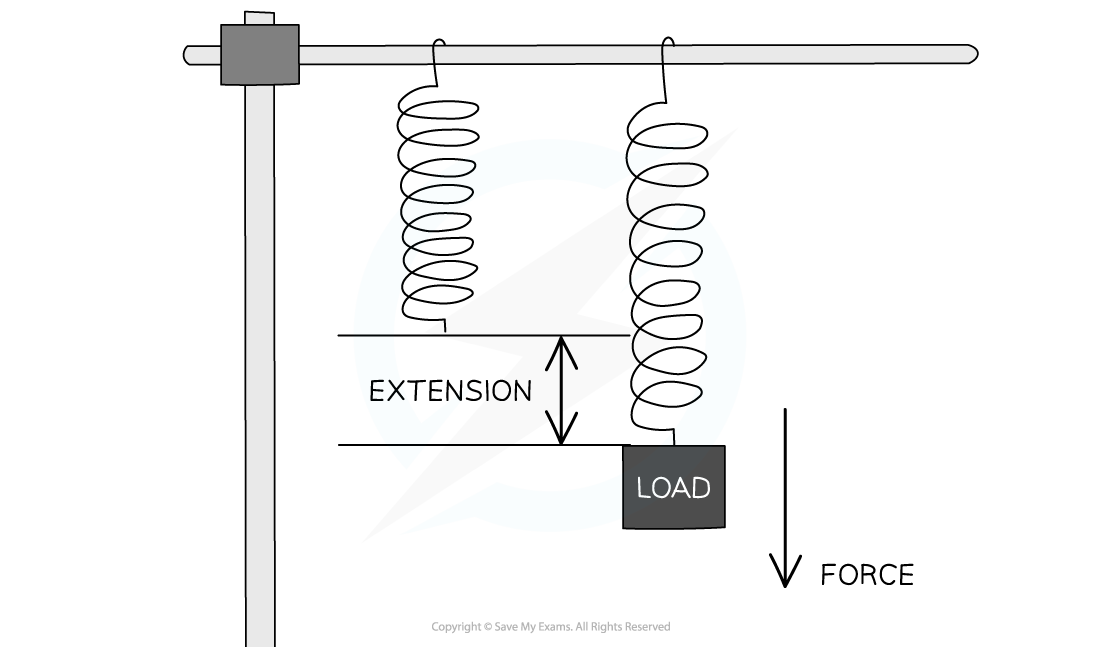
Stretching a spring with a load produces a force that leads to an extension

Force–Extension Graphs

• The way a material responds to a given force can be shown on a force-extension graph
• A material may obey Hooke's Law up to a point
  • This is shown on its force-extension graph by a straight line through the origin

• As more force is added, the graph may start to curve slightly

The Hooke's Law region of a force-extension graph is a straight line. The spring constant is the gradient of that region

• The key features of the graph are:
  • The limit of proportionality: The point beyond which Hooke's law is no longer true when stretching a material i.e. the extension is no longer proportional to the applied force
    • The point is identified on the graph where the line starts to curve (flattens out)

  • Elastic limit: The maximum amount a material can be stretched and still return to its original length (above which the material will no longer be elastic). This point is always after the limit of proportionality
    • The gradient of this graph is equal to the spring constant k

Step 1: Rearrange Hooke's Law to make the spring constant the subject

Step 2: Compare the gradient to the equation in Step 1

• • This graph is length - extension, so the gradient gives:

• • Therefore k is the reciprocal of the gradient

Step 3:  Find the gradient

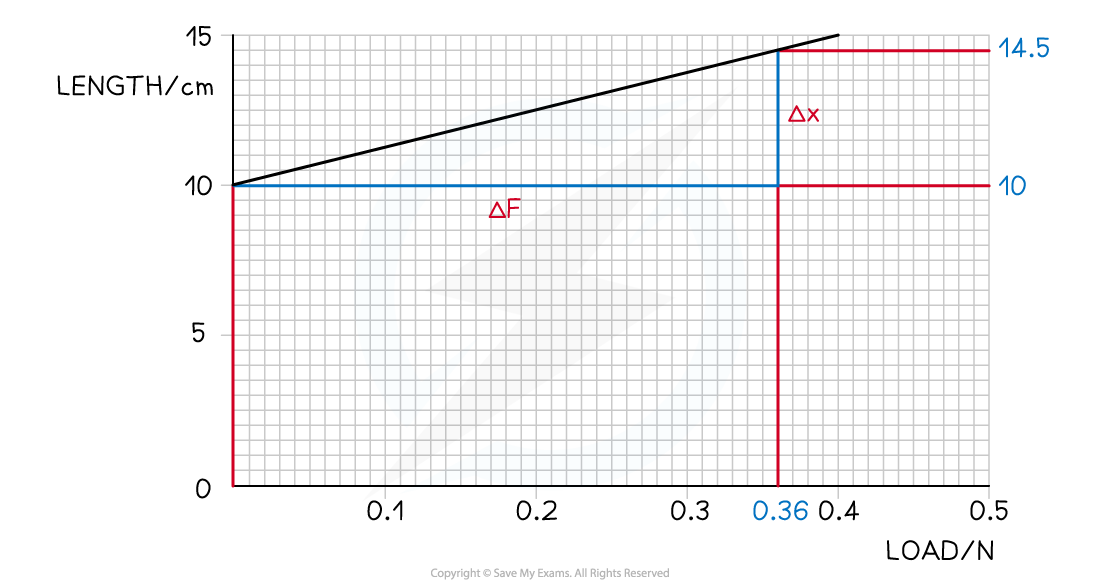
Step 4: Calculate gradient

Step 5: Calculate the spring constant by finding the reciprocal of the gradient

Step 6: Write the answer, including units

• • Spring constant, k = 8.0 N m⁻¹