International A LevelMaths: Statistics 2EdexcelRevision Notes1. Statistical Distributions1.5 Working with Distributions1.5.3 Approximating the Binomial Distribution

Approximating the Binomial Distribution (Edexcel International A Level Maths: Statistics 2)

Revision Note

Test yourself
Dan

Author

Dan

Last updated

Did this video help you?

Normal Approximation of Binomial

When can I use a normal distribution to approximate a binomial distribution?

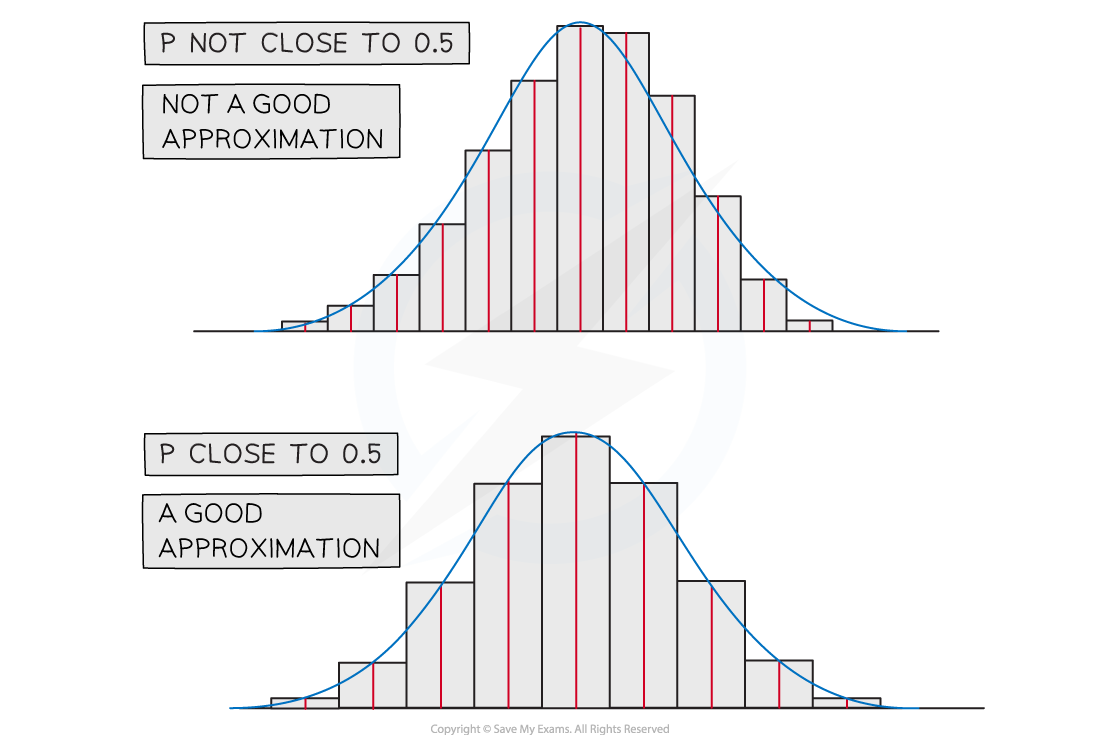
  • A binomial distribution begin mathsize 16px style X tilde straight B left parenthesis n comma p right parenthesis end style can be approximated by a normal distribution begin mathsize 16px style X subscript N tilde straight N left parenthesis mu comma sigma squared right parenthesis end style  provided
    • n is large
    • p is close to 0.5
  • The mean and variance of a binomial distribution can be calculated by:
    • mu equals n p
    • sigma squared equals n p left parenthesis 1 minus p right parenthesis

4-4-2-normal-approximation-of-binomial-diagram-1

Why do we use approximations?

  • If there are a large number of values for a binomial distribution there could be a lot of calculations involved and it is inefficient to work with the binomial distribution
    • These days calculators can calculate binomial probabilities so approximations are no longer necessary
    • However it is easier to work with a normal distribution
      • You can calculate the probability of a range of values quickly
      • You can use the inverse normal distribution function (most calculators don't have an inverse binomial distribution function)

Do I need to use continuity corrections?

  • Yes!
  • As the binomial distribution is discrete and normal distribution  is continuous you will need to use continuity corrections
  • begin mathsize 16px style P left parenthesis X equals k right parenthesis almost equal to P left parenthesis k space minus 0.5 less than X subscript N less than k plus 0.5 right parenthesis end style
  • size 16px P size 16px left parenthesis size 16px X size 16px less or equal than size 16px k size 16px right parenthesis size 16px almost equal to size 16px P size 16px left parenthesis size 16px X subscript size 16px N size 16px less than size 16px k size 16px plus size 16px 0 size 16px. size 16px 5 size 16px right parenthesis
  • size 16px P size 16px left parenthesis size 16px X size 16px less than size 16px k size 16px right parenthesis size 16px almost equal to size 16px P size 16px left parenthesis size 16px X subscript size 16px N size 16px less than size 16px k size 16px minus size 16px 0 size 16px. size 16px 5 size 16px right parenthesis
  • size 16px P size 16px left parenthesis size 16px X size 16px greater or equal than size 16px k size 16px right parenthesis size 16px almost equal to size 16px P size 16px left parenthesis size 16px X subscript size 16px N size 16px greater than size 16px k size 16px minus size 16px 0 size 16px. size 16px 5 size 16px right parenthesis
  • size 16px P size 16px left parenthesis size 16px X size 16px greater than size 16px k size 16px right parenthesis size 16px almost equal to size 16px P size 16px left parenthesis size 16px X subscript size 16px N size 16px greater than size 16px k size 16px plus size 16px 0 size 16px. size 16px 5 size 16px right parenthesis

How do I approximate a probability?

  • STEP 1: Find the mean and variance of the approximating distribution
    • mu equals n p
    • begin mathsize 16px style sigma squared equals n p left parenthesis 1 minus p right parenthesis end style
  • STEP 2: Apply continuity corrections to the inequality
  • STEP 3: Find the probability of the new corrected inequality
    • Find the standard normal probability and use the table of the normal distribution
      • Find the standard normal probability and use the table of the normal distribution
  • The probability will not be exact as it is an approximate but provided n is large and p is close to 0.5 then it will be a close approximation

Worked example

The random variable X tilde straight B left parenthesis 1250 comma 0.4 right parenthesis.

Use a suitable approximating distribution to approximate straight P left parenthesis 485 less or equal than X less or equal than 530 right parenthesis.

1-5-3-normal-approx-to-binomial-we-solution

Did this video help you?

Poisson Approximation of Binomial

When can I use a Poisson distribution to approximate a binomial distribution?

  • A binomial distribution X~B(n, p)can be approximated by a Poisson distribution X subscript p tilde P o open parentheses lambda close parentheses provided
    • n is large ( typically >  50 )
    • p is small
  • The mean of a binomial distribution can be calculated by:
    • lambda equals n p
  • The Poisson distribution is derived from the binomial distribution for conditions where n is becoming infinitely large and p is becoming infinitely small

Do I need to use continuity corrections?

  • No!
  • As both the binomial distribution and Poisson distribution are discrete there is no need for continuity corrections

Worked example

It is known that one person in a thousand who checks a revision website will choose to subscribe. Given that the website received 3000 hits yesterday, use a suitable approximation to find the probability that more than 5 people subscribed.

1-5-3-poisson-approx-of-binomial-we-solution

Did this video help you?

Choosing the Approximation

How will I choose which approximation to use?

  • When deciding what approximating distribution to use first make sure you know the reason why you cannot find the probability using the original distribution  
    • Is the value of n or λ too large?
    • Will it take too long to carry out the calculations?
  • Make sure you know what distribution you are approximating from
    • If your distribution is a binomial distribution, you could either use a Poisson (if p is small) or a normal approximation (if p is close to 0.5)
    • If your distribution is a Poisson distribution, you will use a normal approximation
  • Use the conditions for approximations to decide which approximation is appropriate
  • Calculate the parameters for the approximating distribution

1-5-3-choosing-approximations-diagram-1

Examiner Tip

  • If you are asked to approximate the binomial distribution but are unsure whether to use Poisson or normal, then calculate the mean and see if it is one of the possible values for λ in the table

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.