Uses of the Scalar Product

This revision note covers several applications of the scalar product for vectors – namely, how you can use the scalar product to:

find the angle between vectors or lines
test whether vectors or lines are perpendicular
find the closest distance from a point to a line

How do I find the angle between two vectors?

Recall that a formula for the scalar (or ‘dot’) between vectors $a$ and $b$ is

$a \cdot b = |a| |b| \cos θ$

- where $θ$ is the angle between the vectors when they are placed ‘base to base’
  - that is, when the vectors are positioned so that they start at the same point
- We arrange this formula to make $\cos θ$ the subject:
- To find the angle between two vectors
  - Calculate the scalar product between them
  - Calculate the magnitude of each vector
  - Use the formula to find $\cos θ$
  - Use inverse trig to find $θ$

How do I find the angle between two lines?

To find the angle between two lines, find the angle between their direction vectors

- For example, if the lines have equations $r = a_{1} + s d_{1}$ and $r = a_{2} + t d_{2}$ , then the angle $θ$ between the lines is given by

$θ = \cos^{- 1} (\frac{d_{1} \cdot d_{2}}{|d_{1}| |d_{2}|})$

How do I tell if vectors or lines are perpendicular?

Two (non-zero) vectors $a$ and $b$ are perpendicular if, and only if, $a \cdot b = 0$
- If the a and b are perpendicular then:
  - $θ = 90 ° \Rightarrow \cos θ = 0 \Rightarrow |a| |b| \cos θ = 0 \Rightarrow a \cdot b = 0$
- If $a \cdot b = 0$ then:
  - $|a| |b| \cos θ = 0 \Rightarrow \cos θ = 0 \Rightarrow θ = 90 ° \Rightarrow$ a and b are perpendicular
- For example, the vectors $2 i - 3 j + 5 k$ and $- 4 i - j + k$ are perpendicular since

$(2 i - 3 j + 5 k) \cdot (- 4 i - j + k) = 2 \times (- 4) + (- 3) \times (- 1) + 5 \times 1 = - 8 + 3 + 5 = 0$

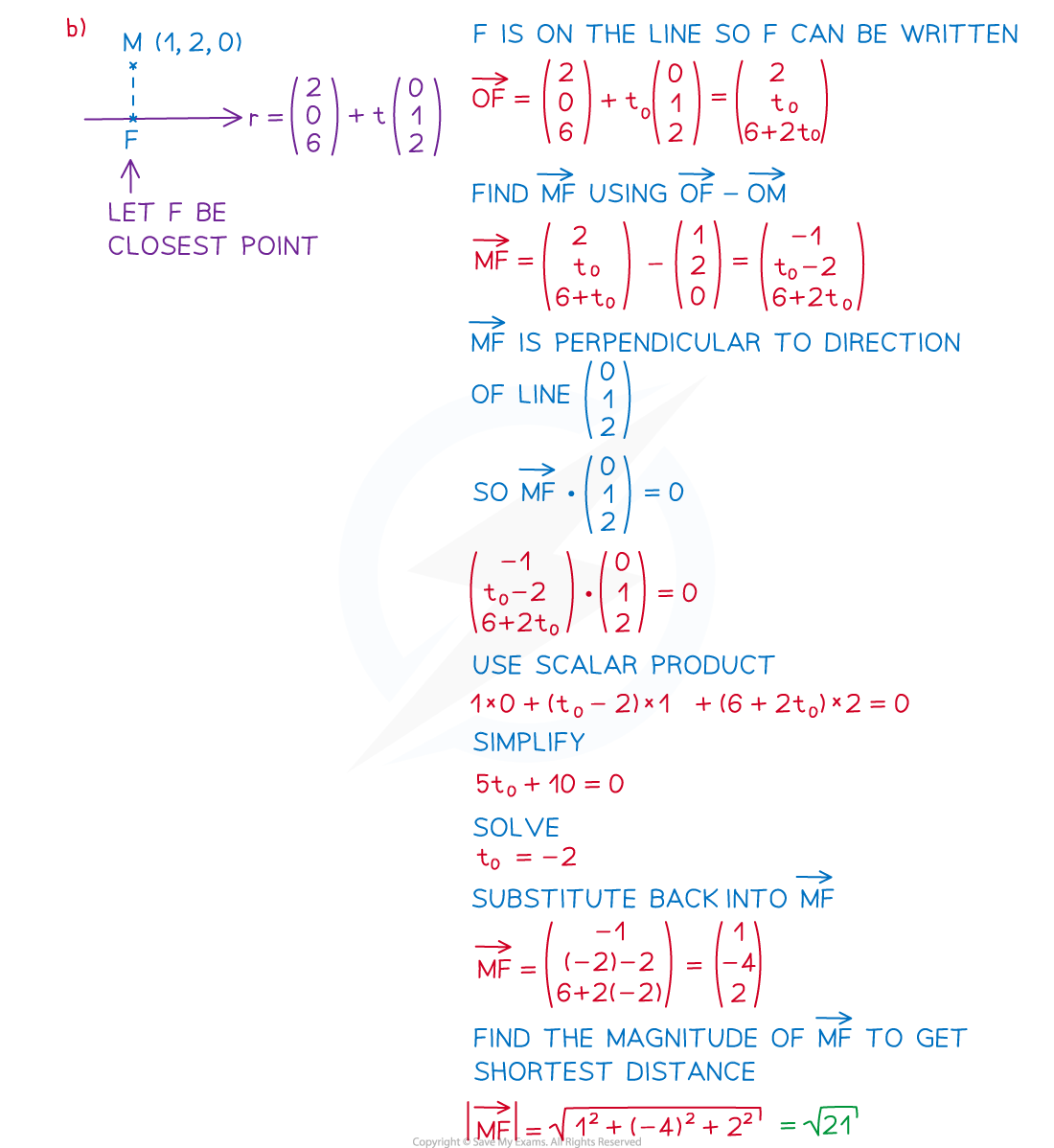
How do I find the shortest distance from a point to a line?

Suppose that we have a line $l$ with equation $r = a + t d$ and a point $P$ not on $l$
Let $F$ be the point on $l$ which is closest to $P$ (sometimes called the foot of the perpendicular)
- Then the line between $F$ and $P$ will be perpendicular to the line $l$
To find the closest point $F$
- Call $f = \vec{OF}$ and $p = \vec{O P}$
- Since $F$ lies on $l$ , we have $f = a + t_{0} d$ , for a unique real number $t_{0}$
- Find the vector $\vec{F P}$ using $p - f$
- $\vec{F P}$ is perpendicular to $d$ so form an equation using $(p - f) \cdot d = 0$
- Solve this equation to find the value of $t_{0}$
- Use the value of $t_{0}$ to find $f$
The shortest distance between the point and the line is the length
Note that the shortest distance between the point and the line is sometimes referred to as the length of the perpendicular

Worked example

7-3-4-uses-of-scalar-product-we-solution-part-1

7-3-4-uses-of-scalar-product-we-solution-part-2

Examiner Tip

It can be easier and clearer to work with column vectors when dealing with scalar products.

Uses of the Scalar Product (Edexcel International A Level Maths: Pure 4)

Revision Note

How do I find the angle between two vectors?

How do I find the angle between two lines?

How do I tell if vectors or lines are perpendicular?

How do I find the shortest distance from a point to a line?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Proof

1.1 Proof by Contradiction

1.1.1 Proof by Contradiction

2. Algebra & Functions

2.1 Partial Fractions

2.1.1 Linear Denominators

2.1.2 Squared Linear Denominators

3. Sequences & Series

3.1 General Binomial Expansion

3.1.1 General Binomial Expansion

3.1.2 General Binomial Expansion - Subtleties

3.1.3 General Binomial Expansion - Multiple

3.1.4 Approximating Values

4. Differentiation

4.1 Further Applications of Differentiation

4.1.1 Connected Rates of Change

4.2 Implicit Differentiation

4.2.1 Implicit Differentiation

5. Integration

5.1 Further Integration

5.1.1 Substitution (Reverse Chain Rule)

5.1.2 Harder Substitution

5.1.3 Integration by Parts

5.1.4 Integration using Partial Fractions

5.1.5 Volumes of Revolution

5.1.6 Adding and Subtracting Volumes

5.1.7 Modelling with Volumes of Revolution

5.1.8 Integration Decision Making

5.2 Differential Equations

5.2.1 General Solutions

5.2.2 Particular Solutions

5.2.3 Separation of Variables

5.2.4 Modelling with Differential Equations

5.2.5 Solving & Interpreting Differential Equations

6. Parametric Equations

6.1 Parametric Equations

6.1.1 Parametric Equations - Basics

6.1.2 Parametric Equations - Eliminating the Parameter

6.1.3 Parametric Equations - Sketching Graphs

6.2 Further Parametric Equations

6.2.1 Parametric Differentiation

6.2.2 Parametric Integration

6.2.3 Parametric Volumes of Revolution

7. Vectors

7.1 Vectors in 2 Dimensions

7.1.1 Basic Vectors

7.1.2 Magnitude & Direction

7.1.3 Vector Addition

7.1.4 Position Vectors

7.1.5 Problem Solving using Vectors

7.2 Vectors in 3 Dimensions

7.2.1 Vectors in 3 Dimensions

7.2.2 Problem Solving using 3D Vectors

7.3 Further Vectors

7.3.1 Equation of a Line in Vector Form

7.3.2 Parallel, Intersecting & Skew Lines

7.3.3 The Scalar ('Dot') Product

7.3.4 Uses of the Scalar Product

Author: Amber