The diagram below shows part of the graph where
.
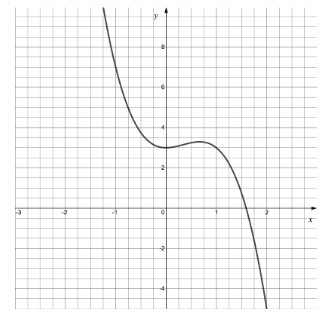
(i) Find
(ii) Find
Write down an interval, in the form , such that
, explain clearly your choice of values for a and b.
Did this page help you?
Exam code: YMA01
The diagram below shows part of the graph where
.

(i) Find
(ii) Find
How did you do?
Write down an interval, in the form , such that
, explain clearly your choice of values for a and b.
How did you do?
Did this page help you?
A solution to the equation is
, correct to two significant figures.
(i) Write down the lower bound, l, and the upper bound, u, of 3.1.
(ii) Assuming is continuous in the interval
, what can you say about the values of
and
?
How did you do?
Did this page help you?
Show that the equation can be rewritten as
How did you do?
Starting with , use the iterative formula
to find values for and
, giving each to four decimal places where appropriate.
How did you do?
Did this page help you?
The graph of where
is shown below. θ is measured in radians and -

Given that .
(i) Find and
.
(ii) Explain how, in this case, the change of sign rule fails to locate a root of in the interval (1.5 , 1.6).
How did you do?
Did this page help you?
A student is trying to find a solution to the equation using an iterative formula.
The student rearranges into the form
.
The diagram below shows a sketch of the graphs of and
.

The student is trying to find the root , starting with an initial estimate
.
Show on the diagram, how the iterative formula will converge and find the root .
Mark the -axis with the positions of
and
.
How did you do?
Did this page help you?
A bypass is to be built around a village.
On the graph below the road through the village is modelled by the line The bypass is modelled by the equation
.

The bypass runs from the origin to the point
Use the iterative formula with
to find the value of
, correct to three significant figures.
How did you do?
(i) Calculate and
where
.
(ii) Hence use the sign change rule to show your answer to part (a) is correct to three significant figures.
How did you do?
Did this page help you?
The game of Tanball is played on a flat table.
A player rolls a ball from a fixed point, at any angle, with the aim of it coming to rest in the winning zone.
A particular player decides to roll the ball at an angle of radians.
This is illustrated by the graph below with the ball being rolled from the origin and the shaded area being the winning zone.

The boundary of the winning zone is given by part of the curve with equation
(i) Using the iterative formula with initial starting value
, find the estimates
and
, writing each to five decimal places.
(ii) Continue using the iterative feature on your calculator to find the value of correct to three significant figures.
(iii) Write down the -coordinate of the point where this player’s ball should cross the winning boundary, give your answer to three significant figures.
How did you do?
Did this page help you?
According to legend, unicorn tears can heal an injury almost instantly.
If a unicorn tear is applied to a burn of initialize size on human skin it will heal according to the model
where is the area of the burn, in square millimeters, at time
seconds after the unicorn tear has been applied.
Show that the equation can be written as
How did you do?
Use the iterative formula with initial value
, to find how many seconds it takes a burn of size
to heal once a unicorn tear is applied .
Give your final answer to three significant figures.
How did you do?
An alternative iterative formula is ,
(i) Using , find
, for the same initial burn size as part (b), giving each to three significant figures.
(ii) Explain how you can deduce whether this sequence of estimates is converging or diverging.
How did you do?
Did this page help you?
The diagram below shows part of the graph where

(i) Find and
, giving your answers to three significant figures.
(ii) Briefly explain the significance of your results from part (i).
How did you do?
One of the solutions to the equation is
, correct to three significant figures.
(i) Write down the upper and lower bound of 2.55.
(ii) Hence, use the sign change rule to confirm that this is a solution (to three significant figures) to the equation .
How did you do?
Did this page help you?
Show that the equation can be rewritten as
How did you do?
Starting with , use the iterative formula
to find a root of the equation , correct to two decimal places.
How did you do?
Did this page help you?
Part of the graph of is shown below, where
is measured in radians.

Explain why the change of sign rule would fail if attempting to locate a root of the function using the values of θ = 1.55 and θ = 1.65.
How did you do?
Did this page help you?
The diagram below shows the graphs of and
.

The iterative formula
is to be used to find an estimate for a root, , of the function
.
Write down an expression for .
How did you do?
Using an initial estimate, , show, by adding to the diagram above, which of the two points (S or T) the sequence of estimates
will converge to.
Hence deduce whether is the
-coordinate of point S or point T.
How did you do?
Find the estimates and
, giving each to three decimal places.
How did you do?
Confirm that correct to three decimal places.
How did you do?
Did this page help you?
The village of Greendale lies on a straight road, as modelled by the line on the graph below. To ease rush hour congestion, a bypass is to be built around Greendale. The path of the bypass is modelled by the equation
.

The bypass runs from the origin to the point .
On the diagram show how using the iterative formula with
will lead to convergence at the point P.
How did you do?
Use the iterative method with
to find the value of
, correct to two decimal places.
How did you do?
Use the sign change rule with the function to show your answer to part (b) is correct to two decimal places.
How did you do?
Did this page help you?
The game of Curveball is played on a flat table.
A player rolls a ball from a fixed point, at any angle, with the aim of it coming to rest in the winning zone.
A particular player decides to roll the ball at an angle of 45°.
This is illustrated by the graph below with the ball being rolled from the origin and the shaded area being the winning zone.

The boundary of the winning zone is given by part of the curve with equation
Use the iterative formula with initial starting value
, to show that the
-coordinate of the point where this player’s ball should cross the winning zone boundary is 0.497 to three significant figures.
How did you do?
Use your answer to part (a) to find the minimum distance the ball should travel for this player to win Curveball.
How did you do?
Did this page help you?
According to legend, a unicorn can heal an injury almost instantly by touching it with its horn.
When a unicorn touches a cut in human skin of length , it will heal according to the model
where is the length of the cut in millimeters, at time
seconds after the unicorn has touched the injury with its horn.
(i) Write down the value would be when the cut is completely healed.
(ii) Show that, for a cut in human skin of length the equation
can be rearranged into the form
How did you do?
Use the iterative formula , with initial value
to find how many seconds it takes a cut of size
to heal once a unicorn has touched it with its horn.
(i) Write down the values of the estimates to four decimal places.
(ii) Give your final answer to two significant figures.
(iii) State the number of iterations required for convergence to two significant figures.
How did you do?
Briefly explain why the model should also restrict the range of to be greater than or equal to zero?
How did you do?
Did this page help you?
The diagram below shows part of the function where
.

Correct to three significant figures, and
.
Explain why using the sign change rule with these values would not necessarily be helpful in finding the root close to .
How did you do?
Using suitable values of x, show that there is a root close to .
How did you do?
Show that the root close to is 0.982, correct to three significant figures.
How did you do?
Did this page help you?
The diagram below shows a sketch of the graphs , and
.

An iterative formula is used to find roots to the equation .
On the diagram above show that the iterative formula
would converge to the root close to when using a starting value of
.
How did you do?
(i) Use in the iterative formula from part (a) to find three further approximations to the root close to
.
Give each approximation correct to three significant figures.
(ii) Comment on your approximations and what they suggest about convergence to the root close to .
How did you do?
Confirm that the root close to is 3.49 correct to three significant figures.
How did you do?
Did this page help you?
The diagrams below show the graphs of four different functions.


Match each graph above with the correct statement below.
The sign change rule with values of and
would indicate a root but has failed due to the discontinuity (asymptote) at
.
The sign change rule with values of and
would indicate no root but has failed because there are two roots in the interval (1 , 5).
The sign change rule with values of and
would indicate no root but fail as there are two roots in the interval (3 , 5).
The sign change rule with values of and
would indicate no root but has failed to find the root as the graph has a turning point at
.
How did you do?
Did this page help you?
The diagram below shows the graphs of and
.

Show on the diagram, using the value of indicated, how an iterative process will lead to a sequence of estimates that converge to the x-coordinate of the point P. Mark the estimates
and
on your diagram.
How did you do?
By finding a suitable iterative formula, use to estimate a root to the equation
correct to two significant figures.
How did you do?
Confirm that your answer to part (b) is correct to two significant figures.
How did you do?
Did this page help you?
The village of Crinkley Bottom lies on a straight road, as modelled by the line on the graph below. Rush hour traffic causes much air pollution in the village so to improve the air quality around Crinkley Bottom a bypass is to be built.
The path of the bypass is modelled by part of the equation .

The bypass is to be built with a roundabout south of the village at the origin and a northern roundabout which re-joins the road through Crinkley Bottom at the point .
On the diagram show how using the iterative formula
with will lead to convergence at the southern roundabout
How did you do?
Use the alternative iterative method
with to find the position of the roundabout at
to four significant figures.
How did you do?
Verify that your answer to part (b) is correct to four significant figures.
How did you do?
Did this page help you?
The game of Logball is played on a flat table.
A player rolls a ball from a fixed point, at any angle, with the aim of it coming to rest within a winning zone.
A particular player decides to roll the ball at an angle of 45°, as illustrated in the graph below, with the ball being rolled from the origin and the shaded area being the winning zone.
The lower boundary of the winning zone has equation ,
The upper boundary of the winning zone has equation ,

Using an appropriate iterative formula with initial value , find the minimum distance this player’s ball needs to travel to stop within the winning zone. Give your answer to two significant figures.
How did you do?
Using another iterative formula with initial value , find the maximum distance this player’s ball can travel yet remain within the winning zone.
Give your answer to two significant figures.
How did you do?
Did this page help you?
According to legend, unicorn tears have magical healing powers.
When a unicorn tear is applied to a bruise of size it will heal according to the model
where is the area of the bruise, in square millimeters, at time
seconds after the unicorn tear is applied.
Show that, for a bruise of initial size , the equation
can be rearranged into the form
How did you do?
Using the equation from part (a) as an iterative formula and initial value find how many seconds it takes a bruise of siae
to heal once a unicorn tear is applied. Give your answer to three significant figures.
How did you do?
It is rumoured that a unicorn tear can heal bruises one-hundred-thousand times faster than they would heal naturally. Approximately how many days would it take a bruise of initial size to heal without a unicorn tear?
How did you do?
Did this page help you?
The diagram below shows part of the graph with equation .

A student searches for a root of the equation . They find that
and that
. The student concludes that there is a root in the interval
.
Explain why the student’s conclusion is incorrect.
How did you do?
Verify that is a solution to the equation
How did you do?
Explain why the sign change rule would fail if searching for the root of the equation
.
How did you do?
Did this page help you?
The function, is defined by
Show that the equation can be written in the form
How did you do?
On the same diagram sketch the graphs of and
.
How did you do?
The equation has a root,
, close to
. The iterative formula
with
is to be used to find
correct to three significant figures.
Show, using a diagram and your answer to part (b), that this formula and initial x value will converge to the root .
How did you do?
(i) Find the values ofand
, giving each correct to three significant figures.
(ii) How many iterations are required before and
agree to two decimal places?
How did you do?
The root lies in the interval
. Write down the values of p and q such that
can be deduced accurate to two decimal places from the interval.
How did you do?
Did this page help you?
Sketch three separate graphs with values of and
, to show how the sign change rule would fail to find a root α in the interval (p , q) for the following reasons:.
(i) Sign change rule indicates a root but there isn’t one due to a discontinuity in the graph.
(ii) Sign change rule indicates no root but there is a root at a turning point.
(iii) Sign change rule indicates no root but there are in fact two roots in the interval p , q.
On each diagram, clearly labelled p, q and the root α.
How did you do?
Did this page help you?
Sketch two separate diagrams to show how an iterative formula of the form
can diverge in two different ways when being used to find an estimate for a root to the equation .
How did you do?
Did this page help you?
The village of Camberwick Green lies on a straight road, as modelled by the line on the graph below. Rush hour traffic through the village causes both congestion and air pollution. To ease congestion and improve the air quality around Camberwick Green a bypass , modelled by part of the equation
is to be built.

The bypass is to be built with a roundabout south of the village at point and a northern roundabout which re-joins the road through Camberwick Green at the point
.
Write down the coordinates of the southern roundabout at point .
How did you do?
(i) Show on the diagram how an iterative method with a starting value () in the interval
will converge to the northern roundabout at point
.
(ii) Use a suitable iterative formula with an appropriate initial value () to find the value of
to five significant figures.
How did you do?
Find the length of road through Camberwick Green that will benefit from the construction of the bypass. Decide on an appropriate unit of measurement.
How did you do?
Did this page help you?
The game of Funcball is played on a flat table. A player rolls a ball from a fixed point, at any angle, with the aim of it coming to rest within a winning zone.
The winning zone is modelled by the function
The lower boundary of the winning zone has equation
The upper boundary of the winning zone has equation ,
A particular player decides to roll the ball at an angle of 45°, as illustrated by the graph below, with the ball being rolled from the origin and the shaded area being the winning zone.

Using iterative formulas with initial values and
as appropriate, find the exact distances between which the ball must stop for this player to win Funcball. Give your answers to two significant figures.
How did you do?
Did this page help you?
According to legend, unicorn tears have magical healing powers.
Without unicorn tears, a bruise of initial size will heal according to the model
where is the area of the bruise, in square millimeters, at time
days since the bruise first appeared.
Use the iterative formula
with to find how many days it takes a bruise to heal without unicorn tears.
Give your answer to three significant figures.
How did you do?
With unicorn tears, a bruise of the same initial size will heal according to the model
where time is measured in seconds.
(i) Find the initial size of the bruise considered in part (a).
(ii) Find how many seconds it takes the same size bruise to heal using unicorn tears.
How did you do?
Using your answer from parts(a) and (b), work out approximately how many times quicker a bruise heals when unicorn tears are used.
How did you do?
Did this page help you?