International A LevelMaths: Pure 3EdexcelRevision Notes5. Integration5.1 Further Integration5.1.2 Reverse Chain Rule

Reverse Chain Rule (Edexcel International A Level Maths: Pure 3)

Revision Note

Test yourself
Paul

Author

Paul

Last updated

Did this video help you?

Reverse Chain Rule

What is the chain rule?

  • The Chain Rule is a way of differentiating two (or more) functions

Notes cr, AS & A Level Maths revision notes

  • In many simple cases the above formula/substitution is not needed

Notes cr_egs, AS & A Level Maths revision notes

  • The same can apply for the reverse – integration

Integrating with reverse chain rule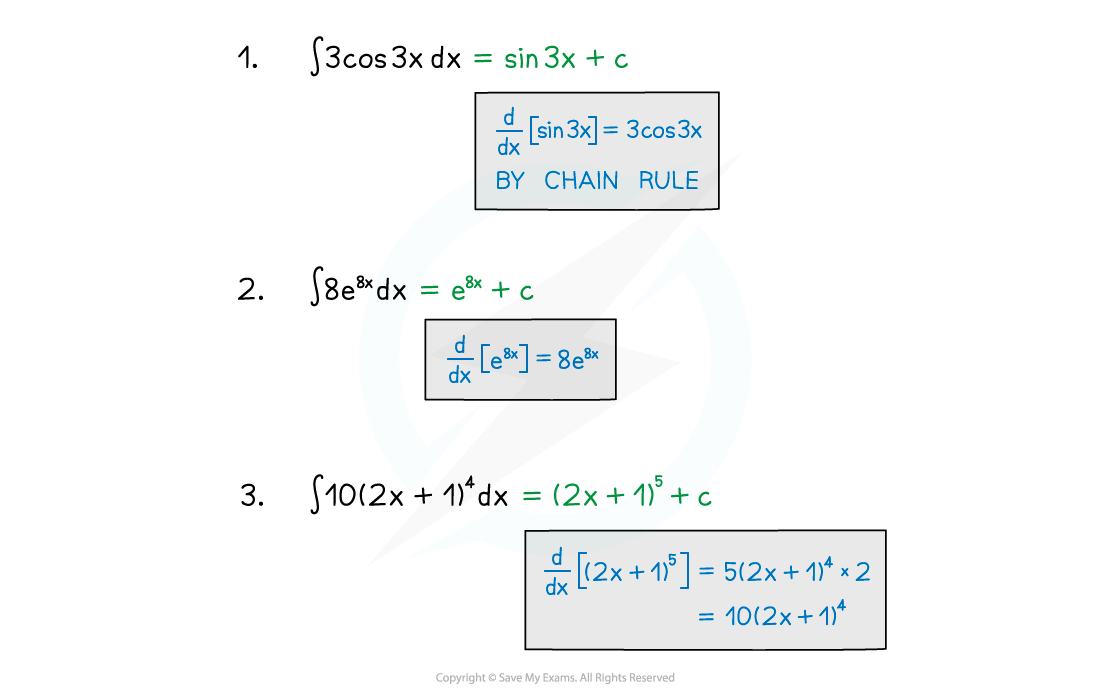Notes rcr_egs, A Level & AS Level Pure Maths Revision Notes

  • In more awkward cases it can help to write the numbers in before integrating

  • STEP 1: Spot the ‘main’ function
  • STEP 2: ‘Adjust’ and ‘compensate’ any numbers/constants required in the integral
  • STEP 3: Integrate and simplify

Notes num_adj1, A Level & AS Level Pure Maths Revision NotesNotes num_adj2, AS & A Level Maths revision notes

Examiner Tip

  • If in doubt you can always use a substitution.
  • Differentiation is easier than integration so if stuck try the opposite, eg. sin and cos are linked (remember that minus!) so if integrating a sin function, start by differentiating the corresponding cos function.
  • Lastly, check your final answer by differentiating it.

Worked example

Example soltn(a), AS & A Level Maths revision notesExample soltn(b), AS & A Level Maths revision notesExample soltn(c), AS & A Level Maths revision notesExample note, AS & A Level Maths revision notes

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:5.1.1 Integrating Other Functions (Trig, ln & e etc)Next:5.1.3 f'(x)/f(x)
    Paul

    Author: Paul

    Expertise: Maths

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams – one of the many reasons he is excited to be a member of the SME team.