e & ln (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Did this video help you?
"e"
What is the number "e" in maths?
e is an irrational number, sometimes called Euler's number
e ≈ 2.718
How do I sketch y = ex?

As other exponential graphs do, y = ex
passes through (0, 1)
has the x-axis as an asymptote
What is the special property of "e"?


y = ex has the particular property
dy/dx = ex
ie for every real number x, the gradient of y = ex is also equal to ex
(see Derivatives of Exponential Functions)
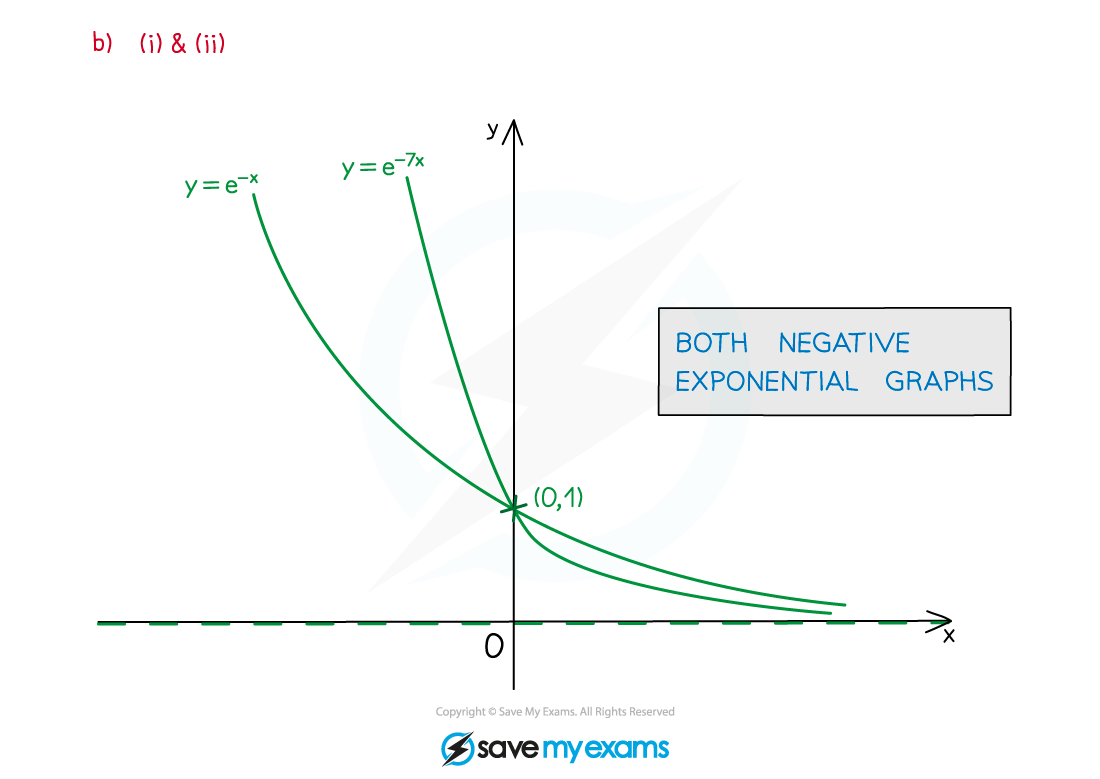
How do I sketch y = e-x?

y = e-x is a reflection in the y-axis of y = ex
They are of the form y = f(x) and y = f(-x)
(see Transformations of Functions - Reflections)
What is exponential growth and decay?

y = Aekx (k > 0) is exponential growth
y = Ae-kx (k > 0) is exponential decay
A is the initial value
k is a (usually positive) constant
“-“ is used in the equation making clear whether it is growth or decay
Worked Example

Did this video help you?
"ln"
What is ln x?
ln is a function that stands for natural logarithm
It is a logarithm where the base is the constant "e"
It is important to remember that ln is a function and not a number
What properties of ln x do I need to know?
Using the definition of a logarithm you can see
is only defined for positive x
As ln is a logarithm you can use the laws of logarithms
Any logarithm can be written in terms of the natural logarithm using the change of base formula
How do I solve equations involving ex & ln x?
The functions
and
are inverses of each other
If
then
If
then
If your equation involves "e" then try to get all the "e" terms on one side
If "e" terms are multiplied, you can add the powers
You can then apply ln to both sides of the equation
If "e" terms are added, try transforming the equation with a substitution
For example: If
then
You can then solve the resulting equation (usually a quadratic)
Once you solve for y then solve for x using the substitution formula
If your equation involves "ln", try to combine all "ln" terms together
Use the laws of logarithms to combine terms into a single term
If you have
then solve
If you have
then solve
Worked Example

Examiner Tips and Tricks
Always simplify your answer if you can
for example,
you wouldn't leave your final answer as
so don't leave your final answer as

Unlock more, it's free!
Did this page help you?