Modelling with Trigonometric Functions (Edexcel International A Level (IAL) Maths) : Revision Note
Did this video help you?
Modelling with Trigonometric Functions
Modelling with trigonometric functions
Various real-life situations can be modelled using trigonometric functions
You need to be able to interpret the equations used in the model
If you need to identify maximum or minimum values of a formula, remember the bounds of the sin and cos functions:
-1 ≤ sin x ≤ 1
-1 ≤ cos x ≤ 1

You may need to simplify trigonometric expressions to make the behaviour of an equation clearer

You may also need to discuss the period of an equation
The period is often indicated by T
For a periodic function in x like sin or cos, the period is how much x has to change by for the function to go through one complete cycle
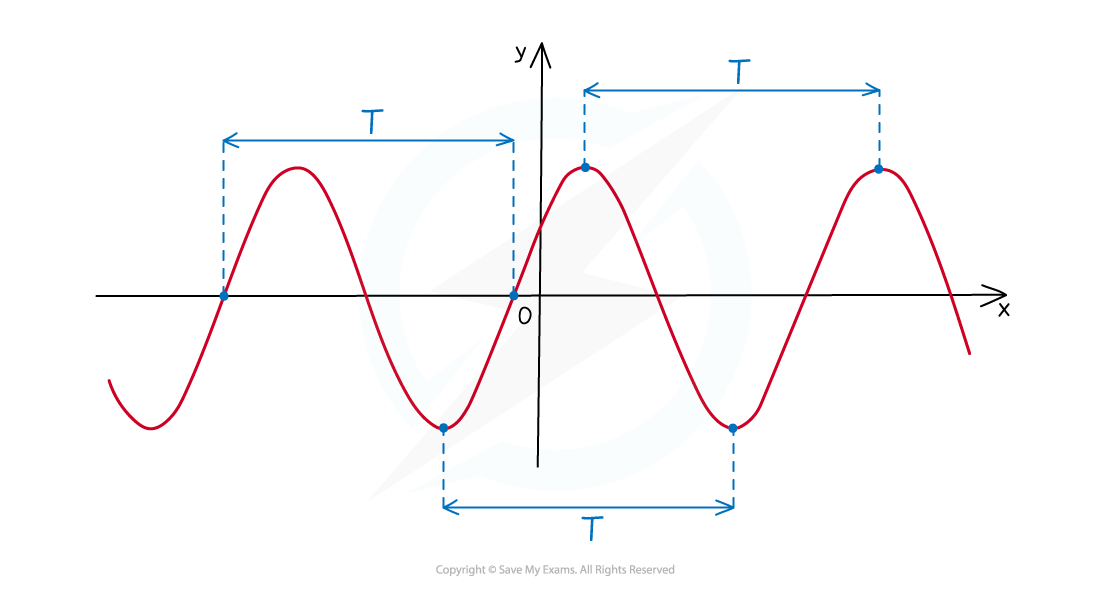
For functions of the form cos (qx+ r) or sin (qx + r) the period T is:

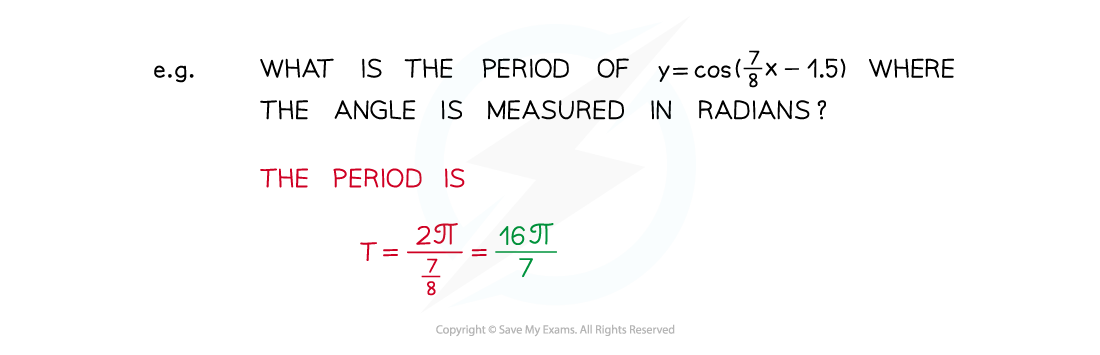
Examiner Tips and Tricks
The variable in these questions is often t for time.
Read the question carefully to make sure you know what you are being asked to solve.
Worked Example


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
