Laws & Change of Base | Edexcel International A Level Maths: Pure 2 Revision Notes 2020

Did this video help you?

Laws of Logarithms

Laws of Logarithms Notes fig1, A Level & AS Maths: Pure revision notes

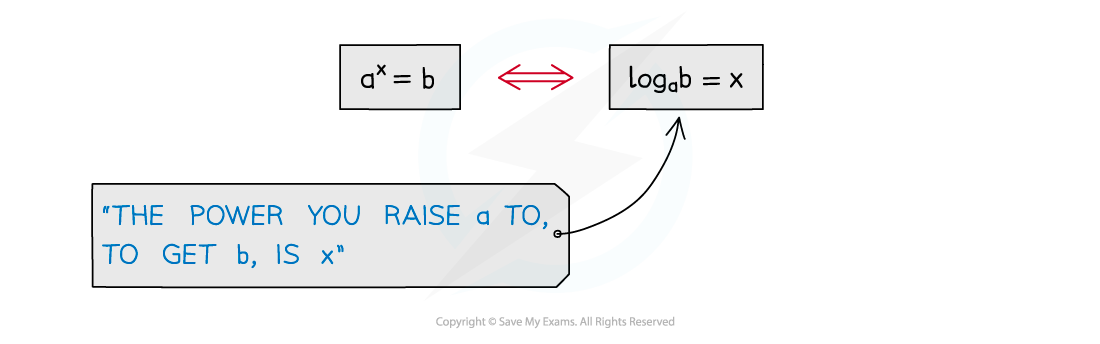
There are many laws or rules of indices, for example
- a^m x aⁿ = a^m+n
- (a^m)ⁿ = a^mn
There are equivalent laws of logarithms (for a > 0)
- $\log_{a} x y = \log_{a} x + \log_{a} y$
- $\log_{a} (\frac{x}{y}) = \log_{a} x - \log_{a} y$
- $\log_{a} x^{k} = k \log_{a} x$

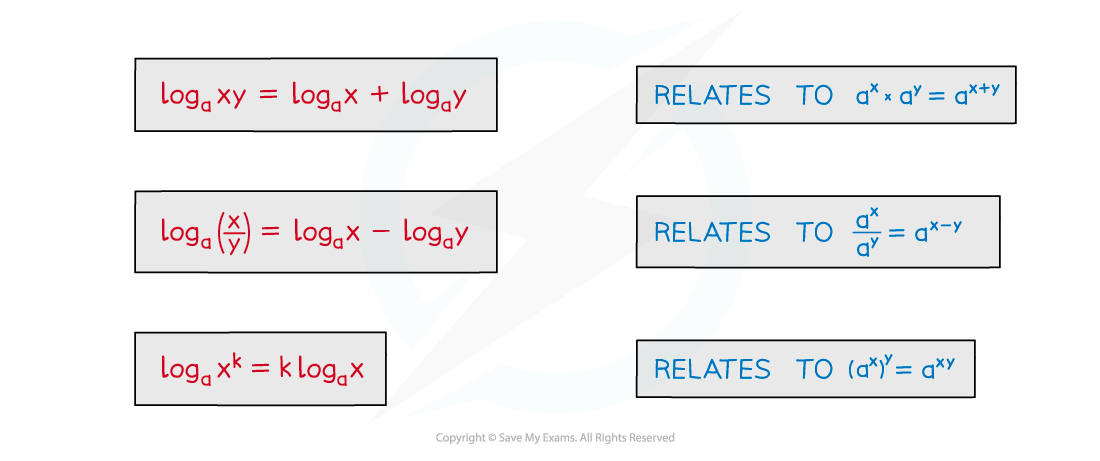
Laws of Logarithms Notes fig2, A Level & AS Level Pure Maths Revision Notes

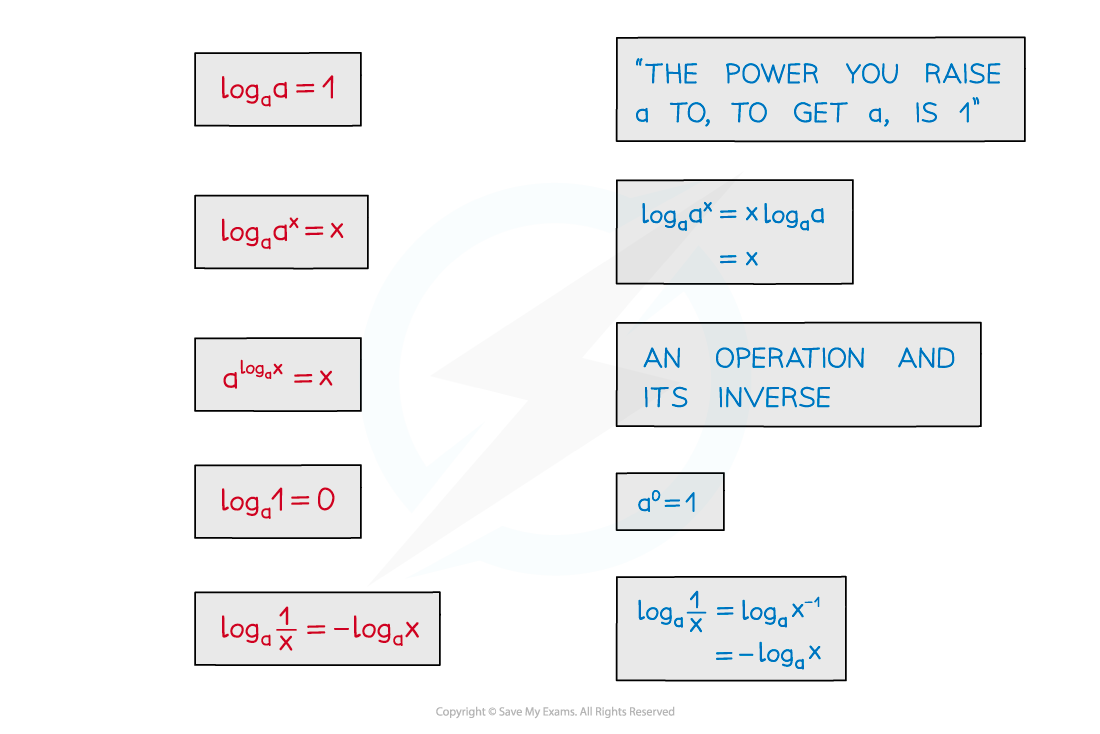
Laws of Logarithms Notes fig3, A Level & AS Level Pure Maths Revision Notes

Laws of logarithms can be used to …
- … simplify expressions
- … solve logarithmic equations
- … solve exponential equations

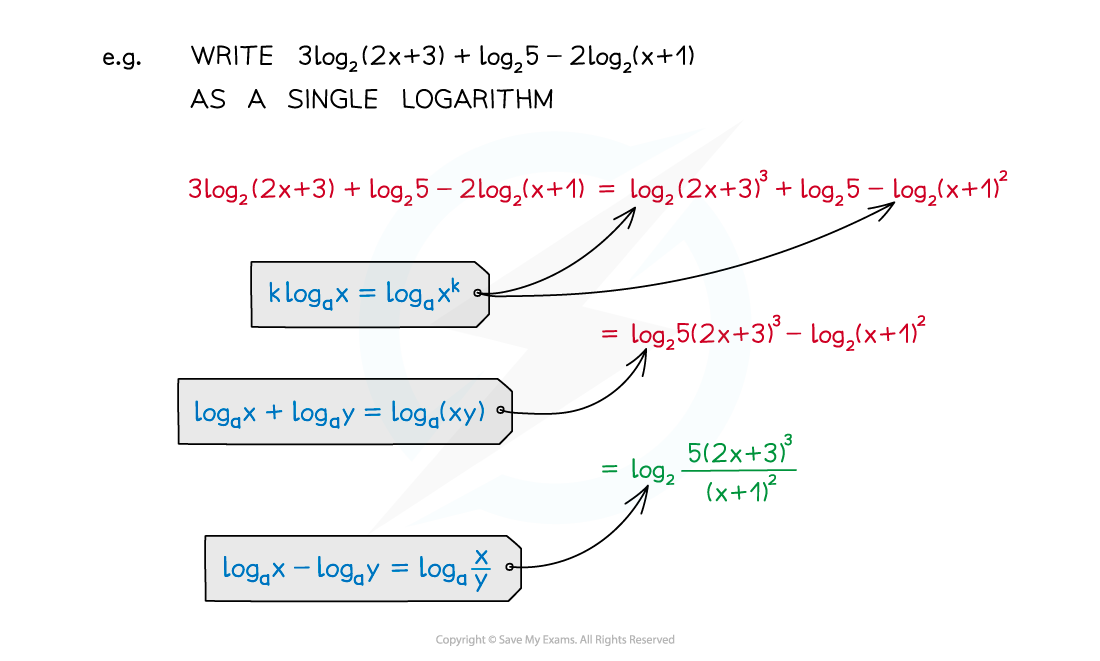
Laws of Logarithms Notes fig4, A Level & AS Level Pure Maths Revision Notes

Remember to check whether your solutions are valid. log (x+k) is only defined if x > -k. You will lose marks if you forget to reject invalid solutions.

Laws of Logarithms Example fig1, A Level & AS Level Pure Maths Revision Notes

Did this video help you?

We can rewrite a logarithm as a multiple of a logarithm of any different positive base using the formula

$\log_{a} x = \frac{\log_{b} x}{\log_{b} a}$

This formula had more use when calculators were less advanced
- Some old calculators only had a button for logarithm of base 10
- To calculate $\log_{5} 7$ on these calculators you would have to enter
  - $\frac{\log_{10} 7}{\log_{10} 5}$

The formula is only needed in a small number of cases
- This is given in the formulae booklet in case it is needed
The formula can be useful when evaluation a logarithm where the two numbers are powers of a common number
- $\log_{4} 8 = \frac{\log_{2} 8}{\log_{2} 4} = \frac{3}{2}$
The formula can be useful when you are solving equations and two logarithms have different bases
- For example, if you have $\log_{3} k$ and $\log_{9} n$ within the same equation
  - You can rewrite $\log_{9} n$ as $\frac{\log_{3} n}{\log_{3} 9}$ which simplifies to $\frac{1}{2} \log_{3} n$
  - Or you can rewrite $\log_{3} k$ as $\frac{\log_{9} k}{\log_{9} 3}$ which simplifies to $2 \log_{9} k$
The formula also allows you to derive and use a formula for switching the numbers:

$\log_{a} x = \frac{1}{\log_{x} a}$