Factor & Remainder Theorem | Edexcel International A Level Maths: Pure 2 Revision Notes 2020

Factor Theorem

The factor theorem is a very useful result about polynomials
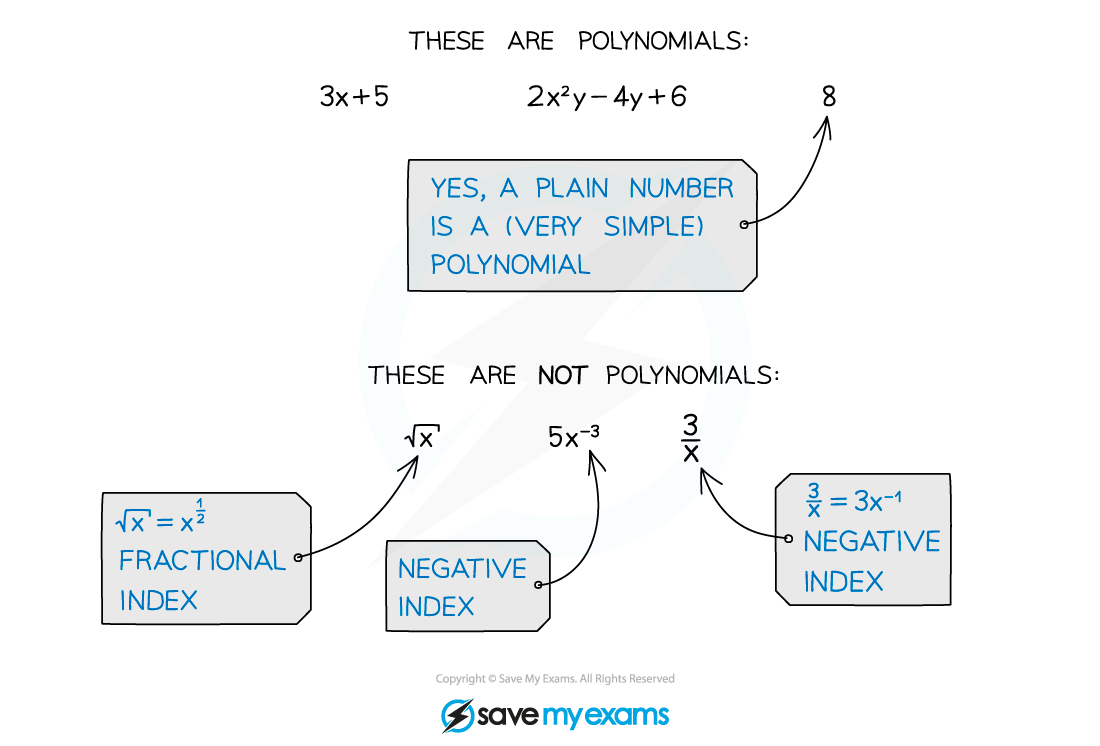
A polynomial is an algebraic expression consisting of a finite number of terms, with non-negative integer indices only

2.5.3 Polynomial not polynomial, Edexcel A Level Maths: Pure revision notes

At A level you will most frequently use the factor theorem as a way to simplify the process of factorising polynomials

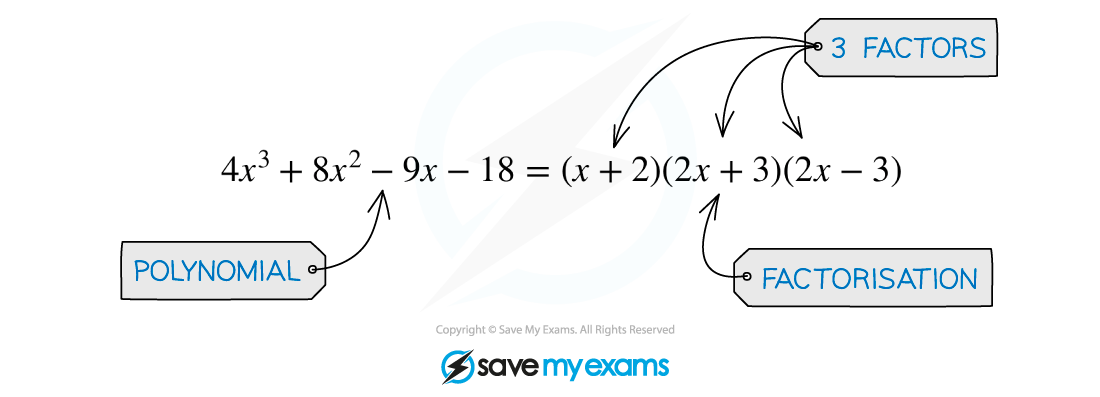
2.5.3 Factorised Polynomial Illustration, Edexcel A Level Maths: Pure revision notes

For a polynomial f(x) the factor theorem states that:
- If f(p) = 0, then (x - p) is a factor of f(x)
AND

2.5.3 Factor Theorem Illustration, Edexcel A Level Maths: Pure revision notes

In an exam, the values of p you need to find that make f(p) = 0 are going to be integers close to zero.
Try p = 1 and -1 first, then 2 and -2, then 3 and -3.
It is very unlikely that you'll have to go beyond that.

2.5.3 Factor Theorem Example, Edexcel A Level Maths: Pure revision notes

The factor theorem is actually a special case of the more general remainder theorem
The remainder theorem states that when the polynomial f(x) is divided by (x - a) the remainder is f(a)
- You may see this written formally as f(x) = (x - a)Q(x) + f(a)
- In polynomial division
  - Q(x) would be the result (at the top) of the division (the quotient)
  - f(a) would be the remainder (at the bottom)
  - (x - a) is called the divisor
- In the case when f(a) = 0, f(x) = (x - a)Q(x) and hence (x - a) is a factor of f(x)– the factor theorem!

If it is the remainder that is of particular interest, the remainder theorem saves the need to carry out polynomial division in full
- e.g. The remainder from ${(x}^{2} - 2 x) \div (x - 3)$ is $3^{2} - 2 \times 3 = 3$
- This is because if f(x) = x²- 2x and a = 3
If the remainder from a polynomial division is known, the remainder theorem can be used to find unknown coefficients in polynomials
- g. The remainder from $(x^{2} + p x) \div (x - 2)$ is 8 so the value of p can be found by solving $2^{2} + p (2) = 8$ , leading to $p = 2$
- In harder problems there may be more than one unknown in which case simultaneous equations would need setting up and solving
The more general version of remainder theorem is if f(x) is divided by (ax - b) then the remainder is $f (\frac{b}{a})$
- The shortcut is still to evaluate the polynomial at the value of x that makes the divisor (ax - b) zero but it is not necessarily an integer

1-2-2-cie-fig1-we-solution-2

Exam questions will use formal mathematical language which can make factor and remainder theorem questions sound more complicated than they are.
Ensure you are familiar with the various terms from these revision notes