Using Moments - Harder (Edexcel International A Level Maths: Mechanics 2)

How do I model ladder problems?

• We can model the ladder as a rod
• There will be two (likely different) reaction forces
  • a vertical reaction force R_f between the bottom of the ladder and the floor
  • a perpendicular reaction between the ladder and the surface that it is leaning on
    • if it is a peg then the reaction force R_p will be perpendicular to the peg
    • if it is a vertical wall then the reaction force R_w will be horizontal
• There could be frictional forces keeping the ladder in equilibrium
  • The frictional force on the floor F_f will act horizontally towards the wall
  • The frictional force on a vertical wall will act vertically upwards
  • The coefficients of friction between the ladder and the floor/wall might be different

How do I solve problems involving ladders?

• Include the weight of the ladder
  • If it is modelled as being uniform then the weight will act at the midpoint of the ladder

• Include any extra weights for any additional objects on the ladder such as a person standing on it
• Form two equations using the horizontal forces and the vertical forces
• If the coefficient of friction is involved then:
  • use F ≤ µR  if the ladder is in equilibrium
  • if the ladder is said to be on the point of slipping it is in limiting equilibrium and so use F = µR

• Form moment equations
  • Useful pivots include the points of contact between the ladder and the floor, wall or peg
  • You will have to use right-angled trigonometry to find the perpendicular distances

• Solve the equations to find any unknown distances, angles, masses or forces

1. 1. the magnitude of the normal reaction force at the wall,
   2. the magnitude of the normal reaction force at the ground,
   3. the magnitude of the frictional force at the ground.

How do I deal with hinges?

•  If one end of a rod is hinged to a surface then that end is fixed to that point but the rod is free to rotate about that point
• There will be a resultant force acting on the rod from the hinge
  • This force will not be perpendicular to the surface – it will be acting at an angle

• Taking moments about the hinge is a good way to avoid including the force from the hinge
• If you are asked to find the magnitude and direction of the force from the hinge:
  • Step 1: Find the horizontal and vertical components of the force
  • Step 2: Find the magnitude by using Pythagoras
  • Step 3: Find the direction by using right-angled trigonometry

• There are two common ways a rod will be held horizontally at a wall:
  • The rod could be without a hinge so that there is contact with the wall which means there is a normal reaction force and a frictional force to stop the rod sliding down the wall
  • The rod could be with a hinge so that there is a resultant force from the hinge acting at an angle of α° to the horizontal which stops the rod rotating about the hinge
  • Splitting the resultant force from the hinge into horizontal and vertical components makes both scenarios mathematically similar

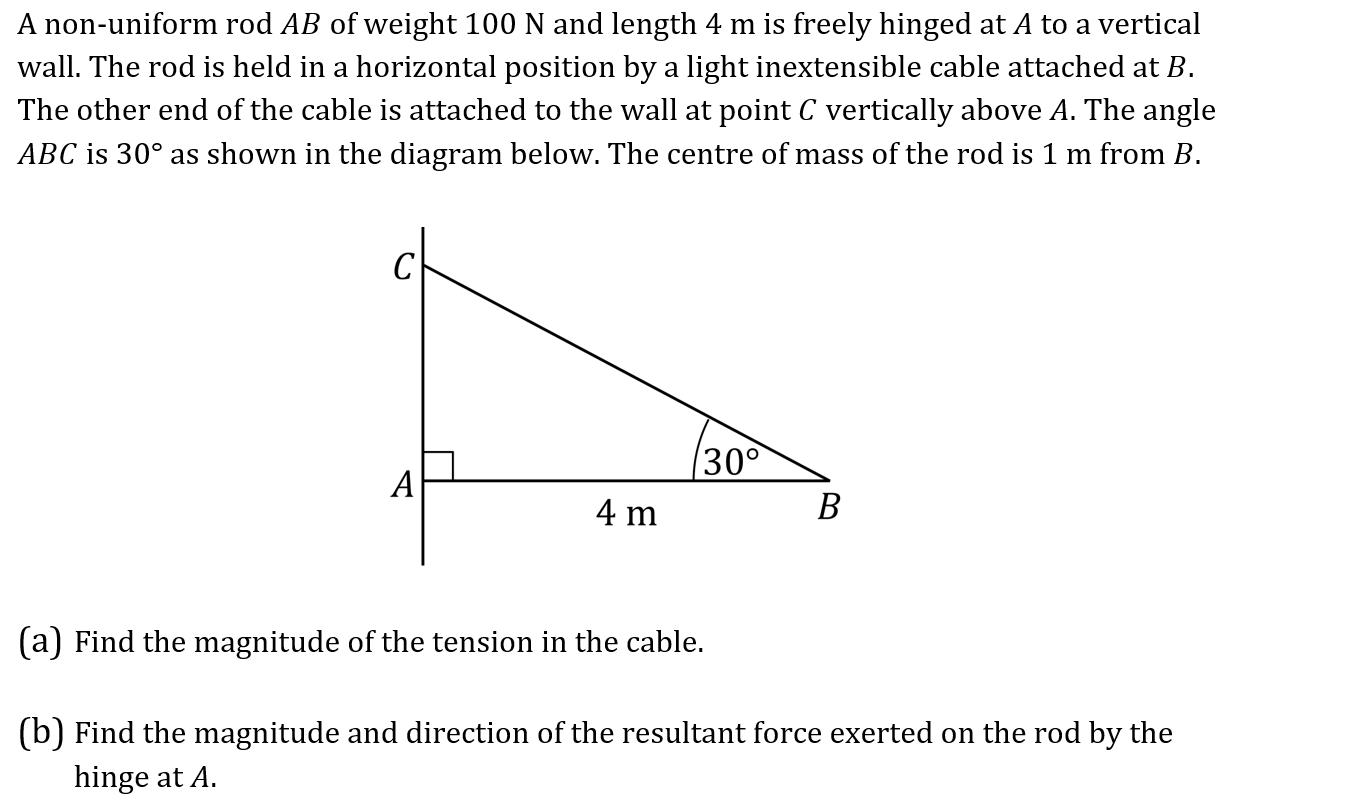
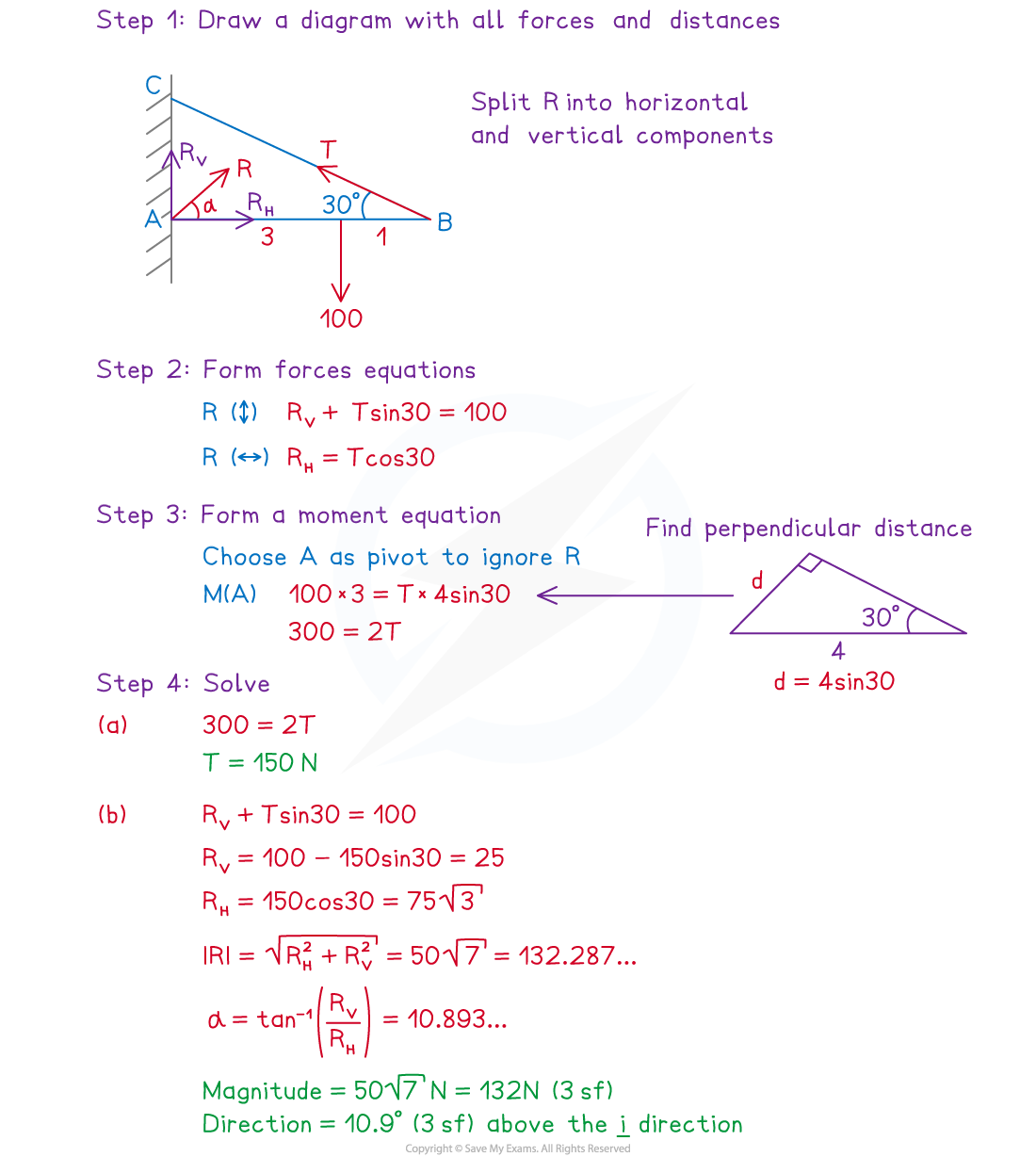
(a)  Find the magnitude of the tension in the cable.

(b)  Find the magnitude and direction of the resultant force exerted on the rod by the hinge at A.