Uniform Laminas (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Did this video help you?
Uniform Laminas
A brief reminder of centre of mass …
The centre of mass is the point at which the total mass of a body (or a system of bodies) can be considered to act as one
What is a lamina?
A lamina is a (3D) body that has one very small dimension compared to the other two dimensions which means the third dimension is negligible and the body can be modelled as a (2D) plane
Common examples include
a sheet of paper, card, wood, metal, plastic, cloth, etc
a wall
What modelling assumptions are used with laminas?
(For this Revision Note) all laminas are uniform
uniform means the mass per unit area (m kg) is equal at every point on the lamina
In the real world a uniform lamina is very difficult to achieve – particularly with natural materials such as timber where knots and other imperfections occur
The cloth on a professional snooker table needs to be as close as possible to a uniform lamina - it should have no imperfections (such as a small tear) if the table and balls are to play as a professional would expect
In Mechanics 2 both uniform (this Revision Note) and non-uniform laminas (Revision Note 2.1.7) are considered
How do I find the centre of mass of a (standard) uniform lamina?
If the shape of a lamina has an axis of symmetry, the position of the centre of mass will be somewhere on that axis
If the shape of a lamina has more than one axes of symmetry, the position of the centre of mass will be the intersection of those axes
The most common shapes – rectangles (including squares), triangles, circles and sectors (including semi-circles) are referred to as standard uniform laminas
How do I find the centre of mass of a triangular lamina?
Triangles are a little more complicated
In any triangle a median is a line joining a vertex to the midpoint of the opposite side
In any uniform triangle the position of the centre of mass
lies
of the way along a median when measured from its vertex.
This is stated in the formulae bookletis the point of intersection of the medians
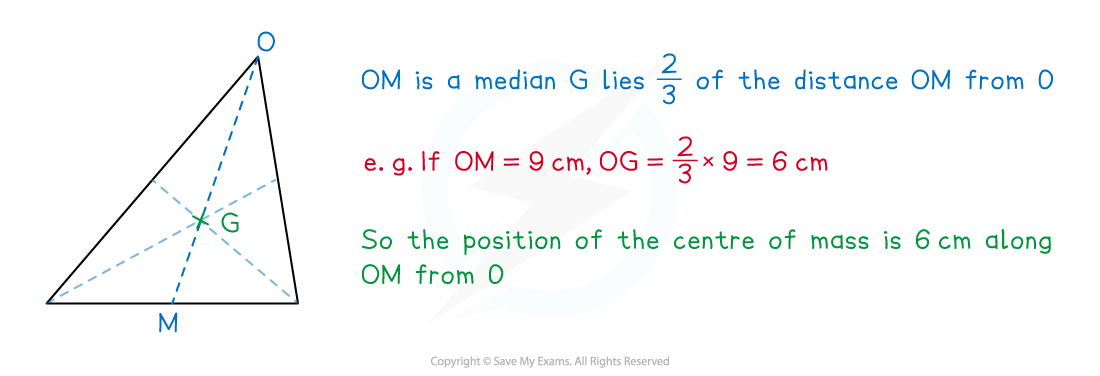
The coordinates of the centre of mass of any uniform triangle can be found if the coordinates of its three vertices are known
The coordinates of the centre of mass of any uniform triangular lamina is the mean of the coordinates of its vertex
This only works for triangles and is not true for all other polygons
In addition to the above, for equilateral and isosceles triangles only
In an equilateral triangle all three medians are also axes of symmetry
In an isosceles triangle one of the medians is an axis of symmetry
The position of the centre of mass will always lie on an axis of symmetry so for both equilateral and isosceles triangles only one median need be used
An axis of symmetry is perpendicular to the side they bisect so any missing lengths can be found using Pythagoras’ theorem and/or basic trigonometry

Worked Example
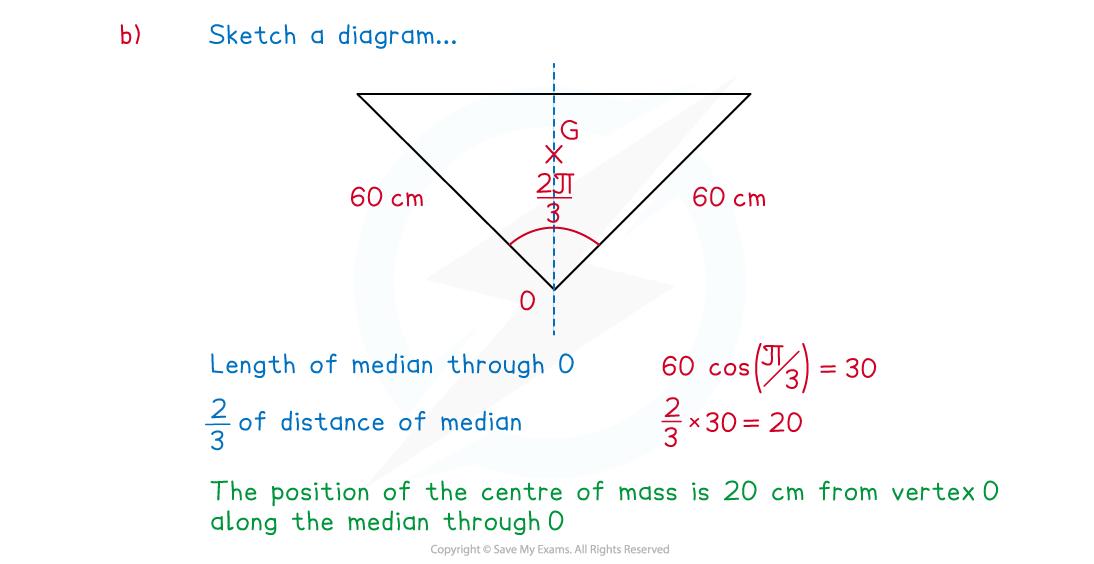
A shop sign is made from a sheet of wood in the shape of an isosceles triangle with its two equal sides of length 60 cm meeting at the vertex O with an angle of radians.
(a) State any modelling assumptions regarding the sheet of wood being used to make the shop sign.
(b) Describe the position of the centre of mass of the shop sign in relation to vertex O.
The shop sign is adapted slightly to make the shape of a sector of a circle with the two equal sides of the isosceles triangle forming two radii of the sector and vertex O becoming the centre of the circle
(c) Describe the new position of the centre of mass of the shop sign in relation to vertex O.
(a) State any modelling assumptions regarding the sheet of wood being used to make the shop sign.

(b) Describe the position of the centre of mass of the shop sign in relation to vertex O.
The shop sign is adapted slightly to make the shape of a sector of a circle with the two equal sides of the isosceles triangle forming two radii of the sector and vertex O becoming the centre of the circle
(c) Describe the new position of the centre of mass of the shop sign in relation to vertex O.

Examiner Tips and Tricks
Sketch diagram(s) or add to any given in a question – this may help you to see an axis of symmetry.
If a triangle is involved, be clear about the type of triangle (and the information about it) you have been given.
Remember that a semi-circle is a sector of a circle with angle π radians at the centre.
Beware! The formula booklet lists the formulae for laminas and frameworks together.

Unlock more, it's free!
Did this page help you?