F = ma - Vector Notation (Edexcel International A Level Maths: Mechanics 1)

How is Newton’s Second Law (N2L) used with vectors?

• The resultant force (F) and acceleration (a) are vectors
  • For forces and motion in two dimensions, F N and a m s^-2  will be made up of two components – a horizontal (x-) component and a vertical (y-) component

• Displacement, velocity and weight are also vector quantities
• Time and mass are scalar quantities
• Vectors appear in bold(non-italic) font in textbooks, on exam papers, etc(i.e. F, a) but in handwriting should be underlined (i.e. F, a)

What notation is used for forces as vectors?

• All vectors are written in i-j format, however you may use column vector notation within your working if you like
• In i-j notation F = ma would look like

• As a column vector F = ma would look like

When do I use  F= ma (N2L) in vector/2D form?

• If vectors/2D are being used this will be clear from the information given in the question – any vector quantities will be given as a column vector or written in i-j notation
• Remember F = ma is used when motion is involved – equations may come from ‘suvat’ (if the acceleration is constant), or using N2L directly; look for (resultant) force, mass and acceleration being involved
• Use  F= ma (N2L in 1D) or an appropriate ‘suvat’ (in 1D) equation to set up and solve separate equations for both the horizontal ( x-) and vertical (y -) components.

How is Newton’s Second Law (N2L) used with problems involving weight?

• Weight is a force, so it is a vector quantity
  • W = mg N where g m s^-2 is the acceleration due to gravity

• Weight always acts vertically downwards so it only acts in the j-direction

                    W = -mgj N                  (g≈ 9.8 m s^-2 )

• Treating the two dimensions separately means weight only needs to be considered when looking at the vertical (y -) direction
• Most 2D/vector problems are based on a bird’s-eye view – the two dimensions being left/right and forwards/backwards, so the up/down (third) dimension where weight would apply, is often not involved

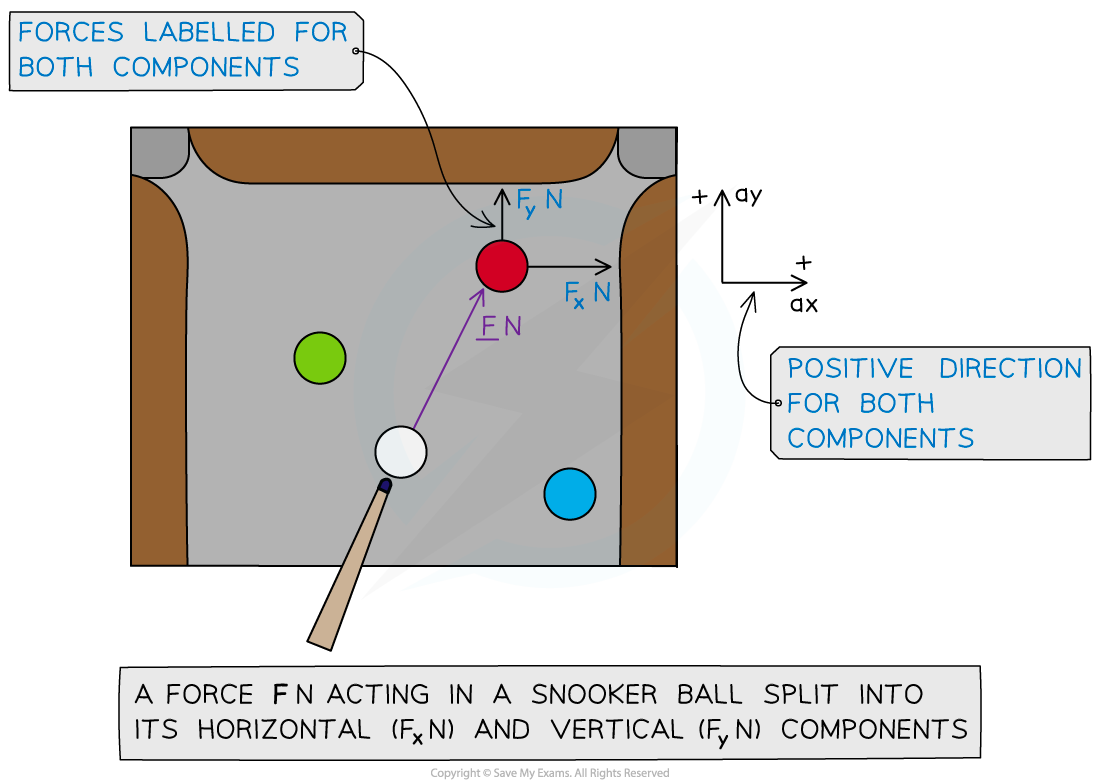
A Force, F, acting on a snooker ball

How do we apply Newton’s Second Law (F = ma) in problems involving vectors?

• Step 1. If necessary, draw a diagram and label all forces acting on the particle(s)
  • label the i and j directions and any other useful information.
  • If a diagram is given, add any missing information to it.

• Step 2. Taking each dimension/component at a time use F = ma
  • If there is more than one particle involved you may have to do this for each

• Step 3. Solve the equations for each component and put the final answers back into vector notation
  • In some harder problems simultaneous equations may arise