Introduction to Prim's Algorithm
What is Prim's algorithm?
- Prim's algorithm is another method of finding a minimum spanning tree in a network
- It can be used when the information for a network is given as a graph or in a matrix
Prim's Algorithm (Edexcel International A Level Maths: Decision 1)
Revision Note
Prim's Algorithm using Edges & Vertices
What are the steps in Prim’s Algorithm when using a graph?
- Prim’s algorithm adds edges from vertices that are already connected to the tree
- Cycles are avoided by only adding edges that do not connect two vertices already in the tree
- STEP 1
Start at any vertex and choose the edge of least weight that is connected to it
- STEP 2
Choose the edge of least weight that is connected to any of the vertices already in the tree
Ensure that it does not connect to a second vertex that is already in the tree-
If there is a choice of edges of equal weight, either can be selected
-
- STEP 3
Repeat STEP 2 until all of the vertices are added to the tree
- STEP 4
List the edges in the minimum spanning tree in the order they were added
Worked example
Consider the network, G, below.
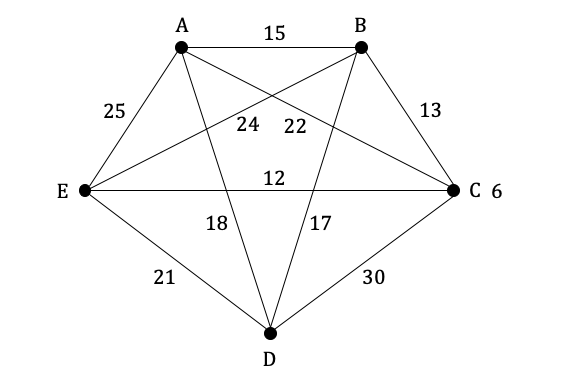
a)
Using Prim’s algorithm, find a minimum spanning tree for G.
- STEP 1
Select a starting vertex (we will use A here, but you could start at any vertex)
Choose the edge of least weight connected to it
AB (15)
- STEP 2
Select the next edge of least weight that is connected to either of the vertices already in the tree
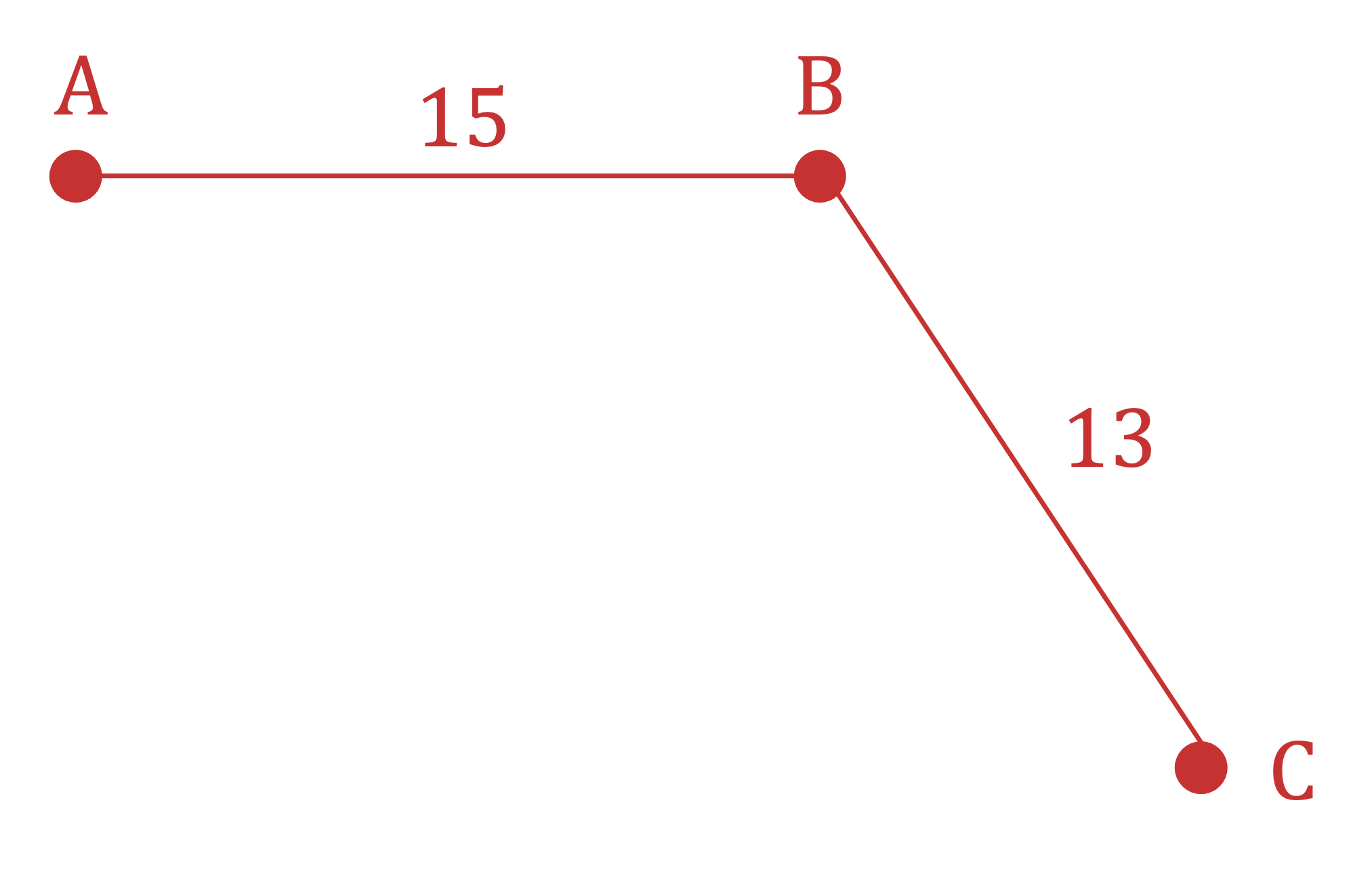
AB (15), BC (13)
- STEP 3
Continue to select the edge of least weight that is connected to any of the other vertices that are already in the tree
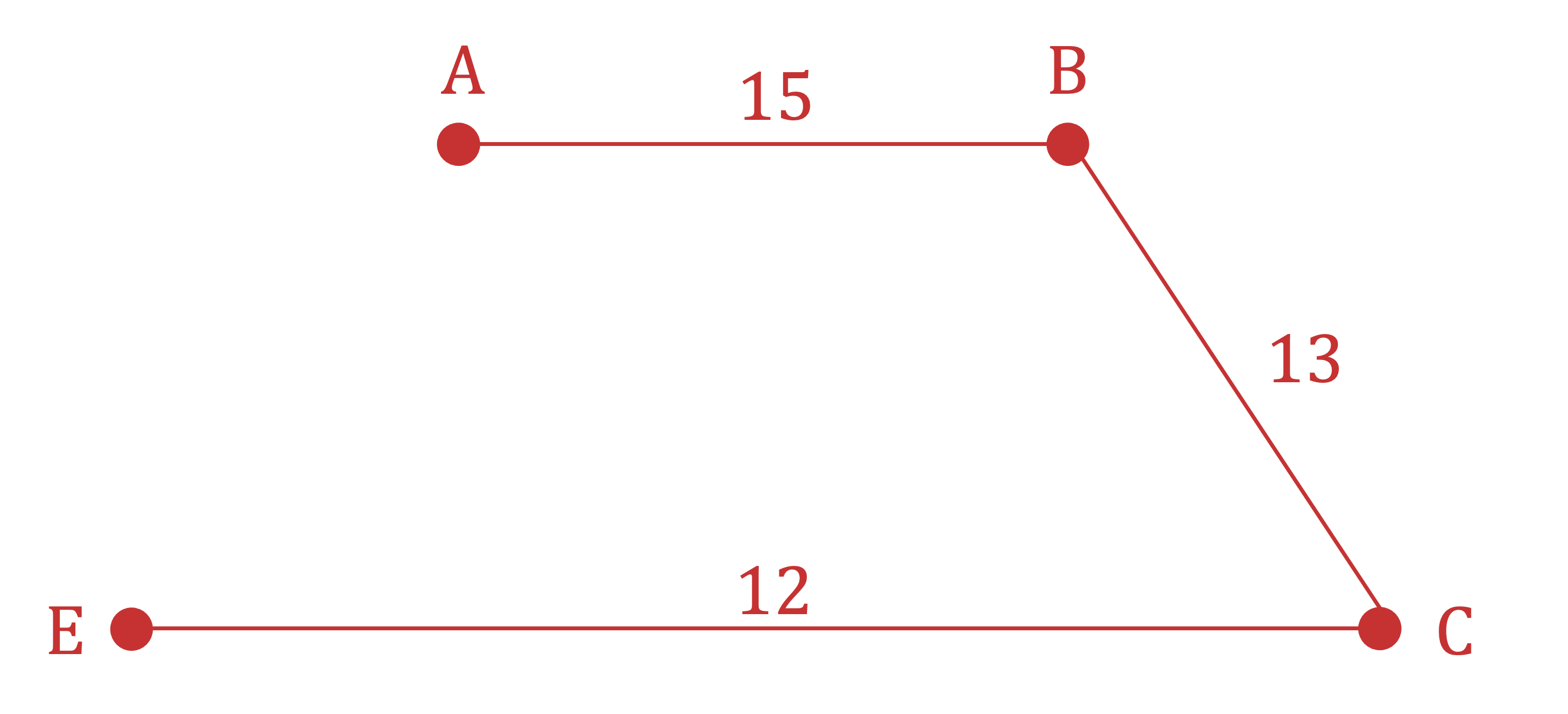
AB (15), BC (13), CE (12)
- STEP 4
Remember to record the order in which the edges were added
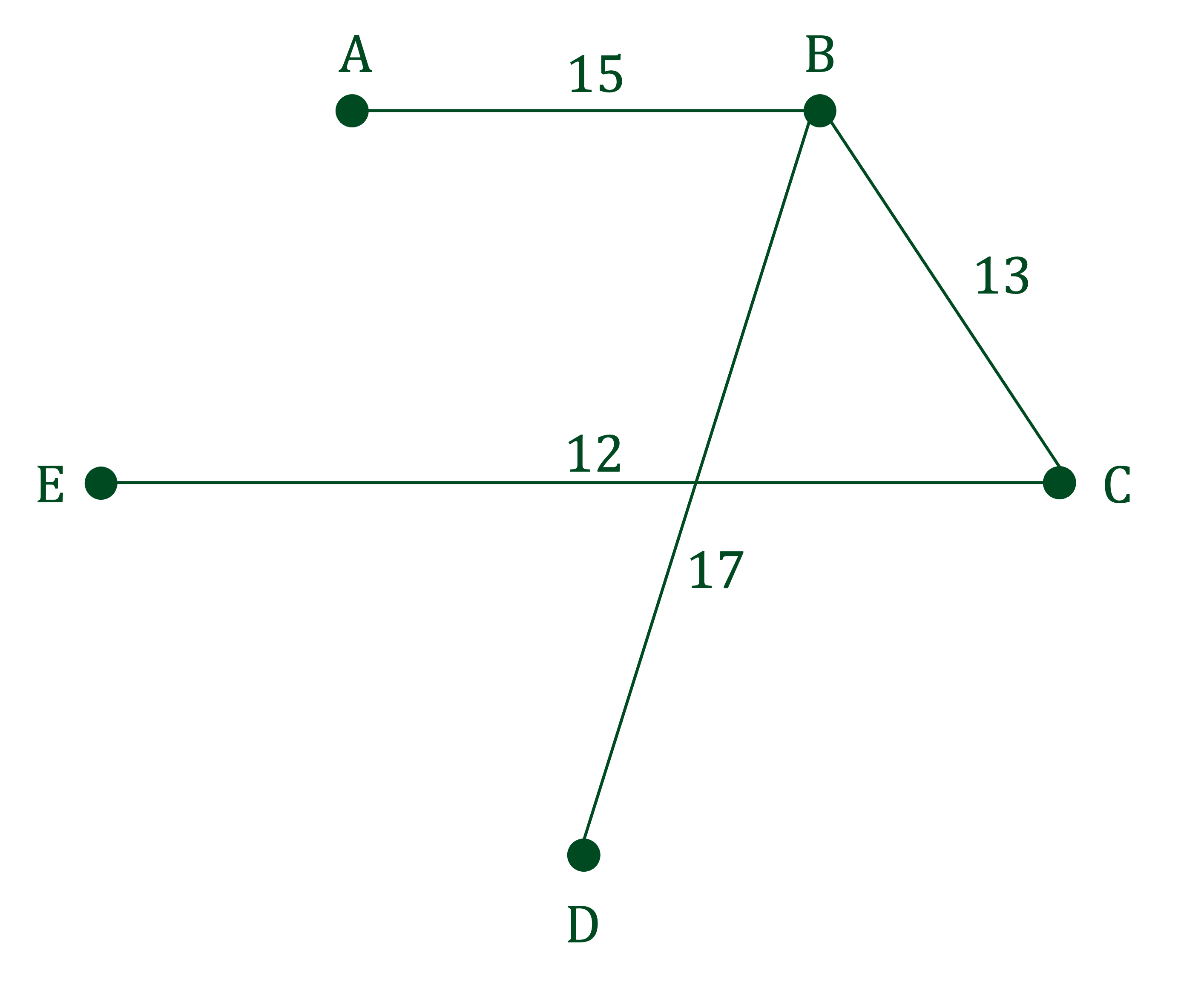
Edges added in the order: AB (15), BC (13), CE (12), BD (17)
b)
State the total weight of the minimum spanning tree.
Add up the weight of the edges in the minimum spanning tree
15 + 13 + 12 + 17 = 57
Total weight = 57
Prim's Algorithm using a Matrix
How do you apply Prim’s algorithm to a matrix?
- A minimum spanning tree can be constructed from a distance matrix
- By looking at the relevant rows in the distance matrix
- By looking at the relevant rows in the distance matrix
- STEP 1
Select any vertex to start from
Cross out the values in the column associated with that vertex
Label the row associated with the vertex 1
- STEP 2
Circle the lowest value in any cell along that row
Add the corresponding edge to the tree
Cross out the remaining values in the column of the cell that you have circled
- STEP 3
Label the row associated with the same vertex as the column in STEP 2 with the next number
- STEP 4
Circle the lowest value in any cell along any of the rows that have been labelled
Add the corresponding edge to the tree
Cross out the remaining values in the column of the cell that you have circled
- STEP 5
Repeat STEPS 3 and 4 until all vertices have been added to the tree
- Some versions of Prim's algorithm using a matrix will cross out rows and label columns
- Either version will work to find a minimum spanning tree
Examiner Tip
- Look out for questions that ask you to minimise the cost or length etc. from a network
- They are implying that they want you to find a minimum spanning tree
- Be careful not to confuse Prim's algorithm with the Nearest Neighbour algorithm
Worked example
The adjacency matrix of a network, is shown below.
| A | B | C | D | E | |
| A | - | 15 | 22 | 18 | 25 |
| B | 15 | - | 13 | 17 | 24 |
| C | 22 | 13 | - | 30 | 12 |
| D | 18 | 17 | 30 | - | 21 |
| E | 25 | 24 | 12 | 21 | - |
a)
Starting from vertex A, use Prim’s algorithm on the table to find and draw a minimum spanning tree for the network. Show each step of the process clearly.
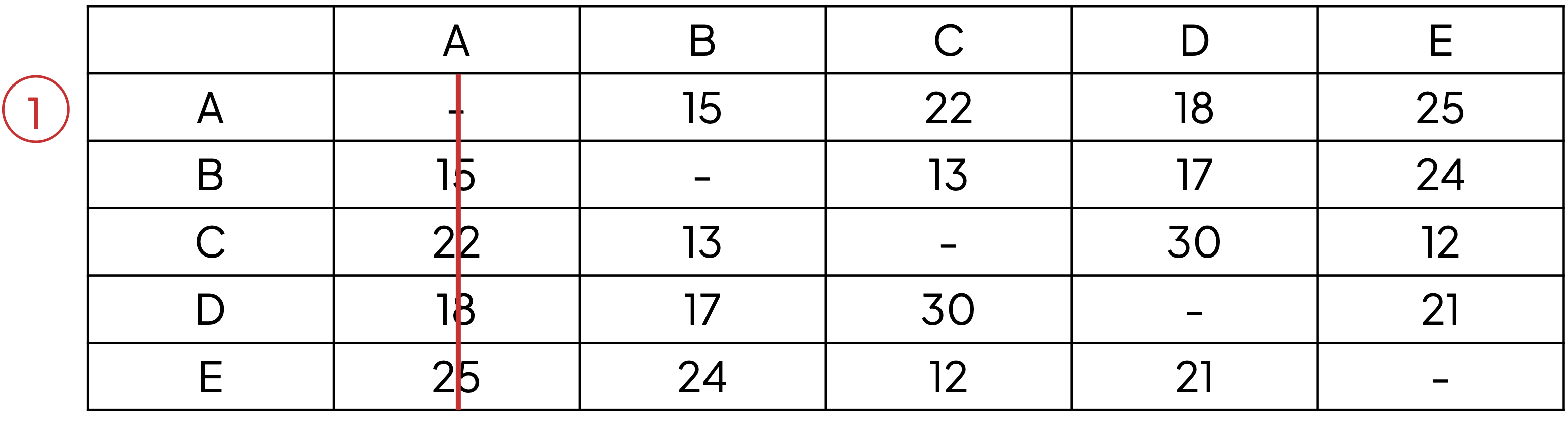
- STEP 1
We'll start here with vertex A, although you could start with any vertex
Label the row for vertex A as '1'
Cross out the values in column A
- STEP 2
Circle the edge of least weight in row 1 and record which edge it is (here it is B)
Delete the remaining values in column B
AB (15)
- STEP 3
Label the row for vertex B as '2'
- STEP 4
Circle the edge of least weight out of all the entries in rows 1 and 2, remembering to record the edge
Cross out the remaining values in the column of that circled edge
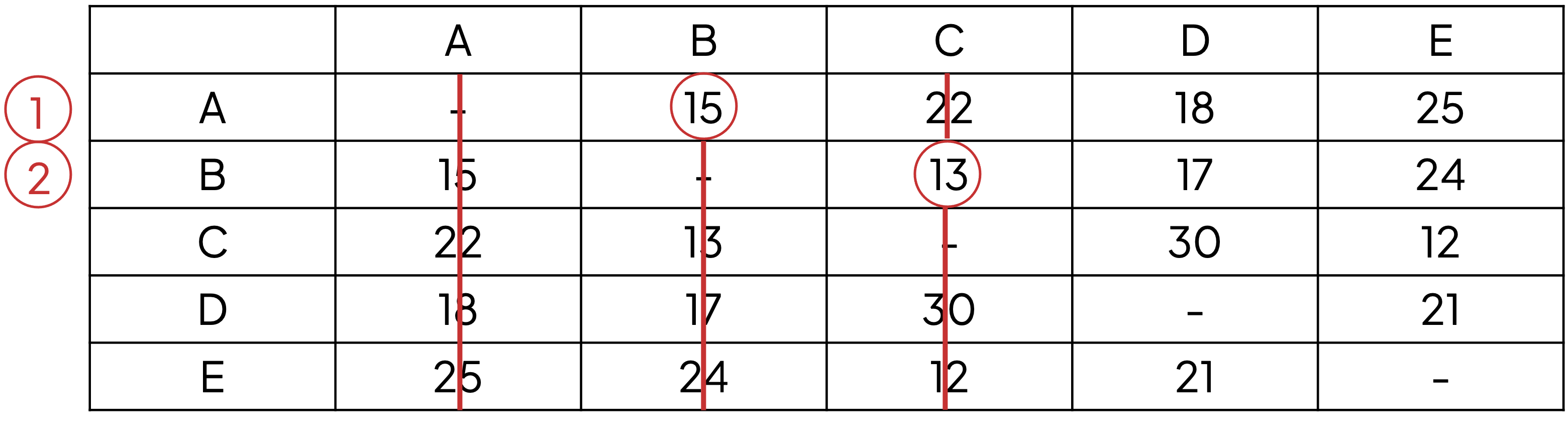
AB (15), BC (13)
- STEP 5
Repeat Steps 3 and 4 until all vertices are added
- STEP 3
Label the row for vertex C as '3'
- STEP 4
Circle the edge of least weight in rows 1 to 3, remembering to record the edge
Delete the remaining values in column E
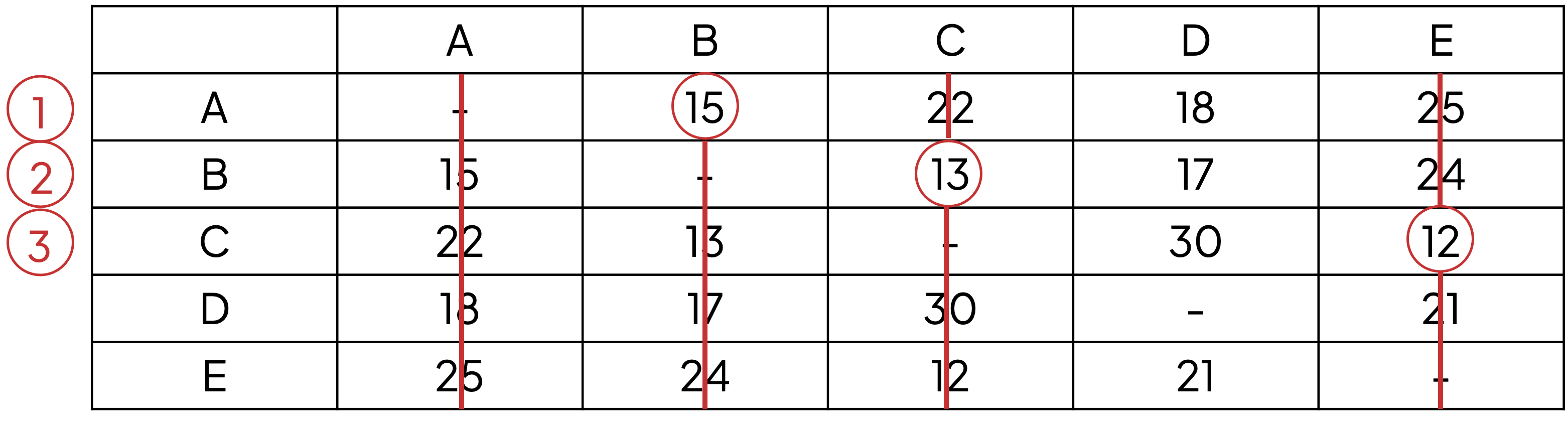
AB (15), BC (13), CE (12)
- STEP 3
Label the row for vertex E as '4'
- STEP 4
Circle the edge of least weight in rows 1 to 4, remembering to record the edge
Delete the remaining values in column D
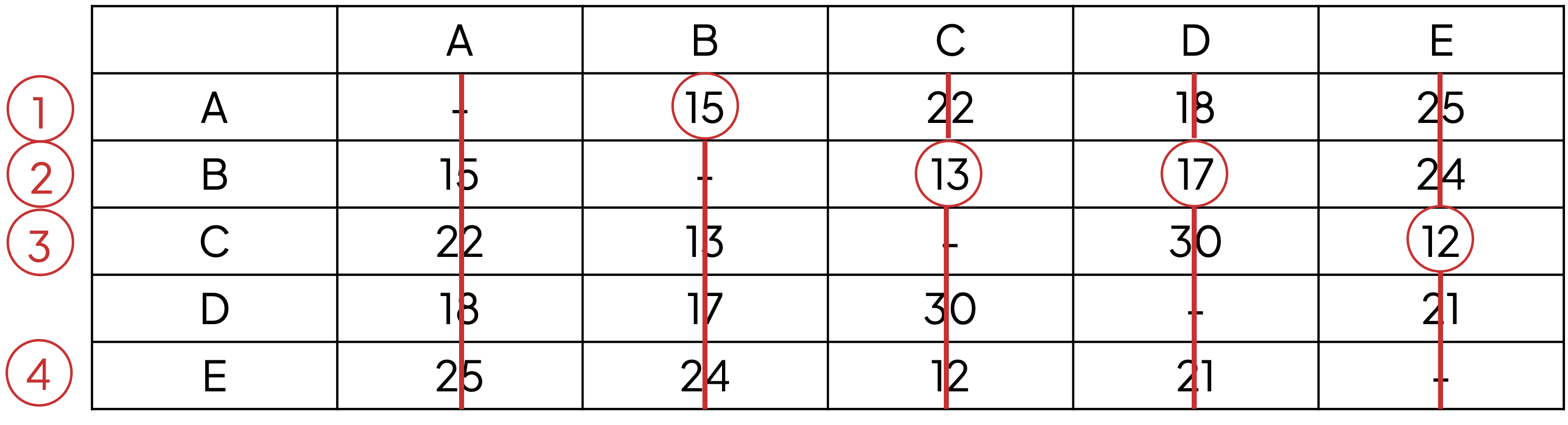
AB (15), BC (13), CE (12), BD (17)
All vertices have been selected
You should have a list of the order in which the edges were selected
Edges added in the order: AB (15), BC (13), CE (12), BD (17)
b)
State the total weight of the minimum spanning tree.
Add up the weights of the edges in the minimum spanning tree.
15 + 13 + 12 + 17 = 57
Total weight = 57
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?