The graph G shown below is a connected, unweighted, directed graph with 5 vertices.
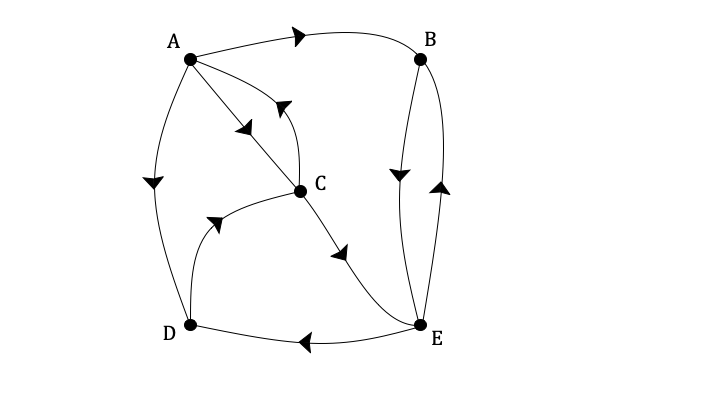
a)
Write down a cycle, starting at vertex A and visiting exactly 2 other vertices.
A cycle starts and ends at the same vertex, with no other vertex visited more than once
Two other vertices (from the 4 possibilities) need to be included
The directed edges mean, in this case, there is only one such cycle
ADCA
b)
Write down a path, consisting of more than one edge, that starts at vertex A and ends at vertex B.
A path is a walk that does not repeat any nodes
You must only traverse edges in the directions indicated
ADCEB
A path does not have to visit every node (so ACEB or ABEB, for example, are also acceptable)









