Modulus & Argument (Edexcel International A Level Further Maths)

Revision Note

Written by: Mark Curtis

Reviewed by: Dan Finlay

Argand Diagrams

What is an Argand diagram?

An Argand diagram is a 2D Cartesian grid used to visualise complex numbers
The complex number $x + y i$ is represented by the point with coordinates $(x, y)$
- The real part is measured along the x -axis
  - called the real axis, written "Re"
- The imaginary part is measured along the y -axis
  - called the imaginary axis, written "Im"
Complex numbers can be thought of as points, or as vectors from the origin

8-2-1-argand-diagrams---basics-diagram-1

8-2-1-argand-diagrams---basics-diagram-2

Examiner Tips and Tricks

If asked to sketch an Argand diagram, it does not need to be to scale (plotted), but should roughly show the correct positions.

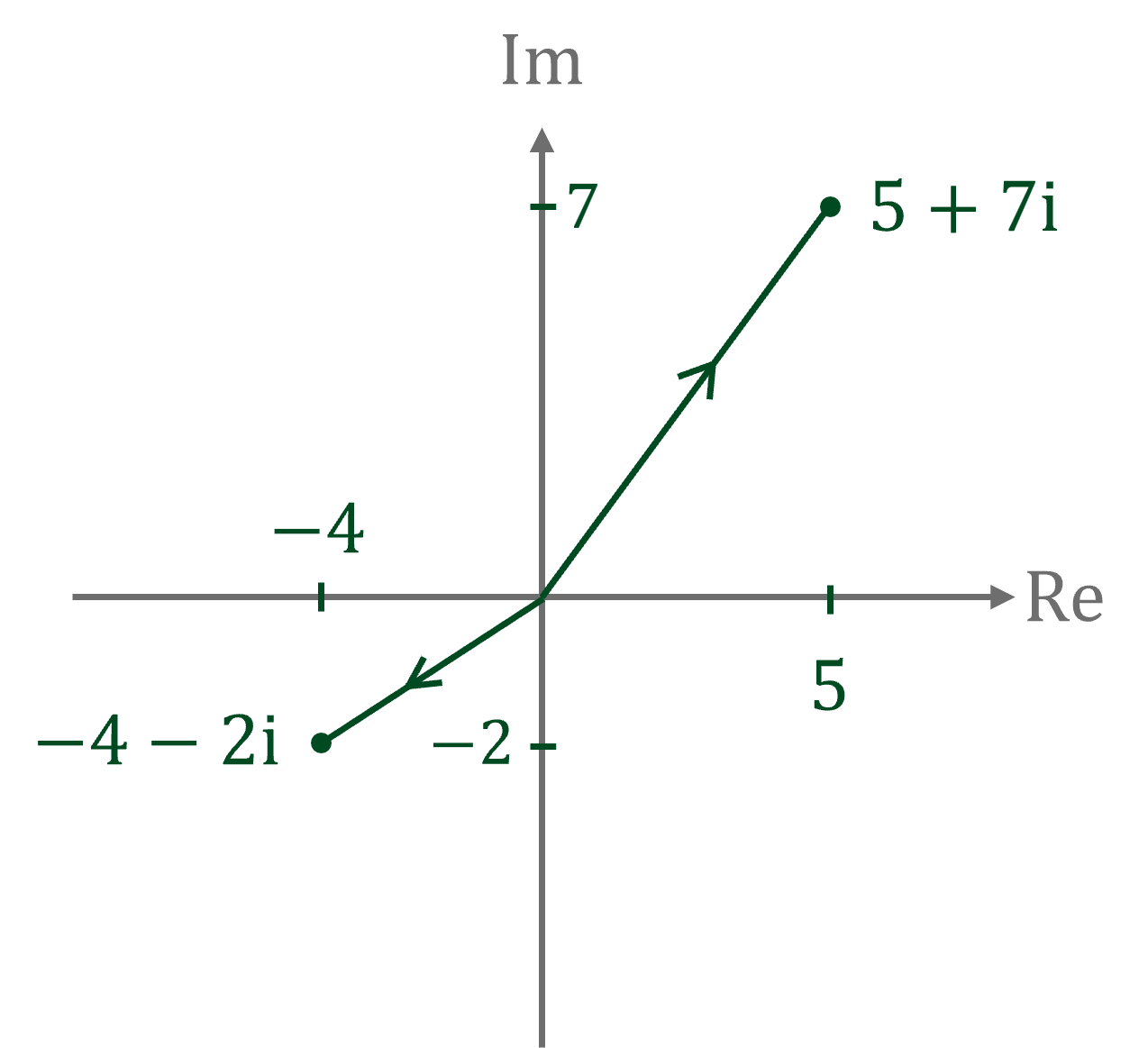
Worked Example

Sketch, on the same Argand diagram, the complex numbers $5 + 7 i$ and $- 4 - 2 i$ .

Two complex numbers plotted on an Argand diagram

Modulus & Argument

How do I find the modulus of a complex number?

The modulus of a complex number is its distance from the origin on an Argand diagram
- It is written $|z|$
- If $z = x + i y$ , then by Pythagoras' theorem
  - $|z| = \sqrt{x^{2} + y^{2}}$
A modulus is always positive or zero
- It cannot be negative
For example
- $| 3 + 4 i | = \sqrt{3^{2} + 4^{2}} = 5$
- $| 1 - i | = \sqrt{1^{2} + {(- 1)}^{2}} = \sqrt{2}$
- $| - 5 | = 5$
- $| 8 i | = 8$
- $| 0 + 0 i | = 0$

What rules does the modulus follow?

Helpful modulus rules are:
- $| z_{1} z_{2} | = | z_{1} | | z_{2} |$
- $|\frac{z_{1}}{z_{2}}| = \frac{|z_{1}|}{|z_{2}|}$
- $| z | = | z * |$
- $z z * = z * z = | z |^{2}$
  - Proved using $z = x + y i$ and $z * = x - y i$
Be careful: $|z_{1} + z_{2}| \neq |z_{1}| + | z_{2} |$
- For example, $z_{1} = 3 + 4 i$ and $z_{2} = - 3 + 4 i$
  - $|z_{1}| = \sqrt{3^{2} + 4^{2}} = 5$ and $| z_{2} | = \sqrt{{(- 3)}^{2} + 4^{2}} = 5$
  - so $| z_{1} | + | z_{2} | = 10$
  - but $z_{1} + z_{2} = 8 i$ so $|z_{1} + z_{2}| = 8$

How do I find the argument of a complex number?

A diagram showing the different cases of arguments of a complex number

The argument of a complex number is the angle in radians that it makes to the positive real axis
- It is written as $\arg z$
- The positive direction is anticlockwise
The range normally used is $- π < \arg z \leq π$
- This is called the principal range
- The sign of the angle depends on the quadrant:
  - The 1^st quadrant is positive acute
  - The 2^nd quadrant is positive obtuse
  - The 3^rd quadrant is negative obtuse
  - The 4^th quadrant is negative acute
Arguments are found by
- drawing a sketch
- forming a right-angled triangle
- using trigonometry
The argument of the origin, $\arg (0 + 0 i)$ , is undefined
- No angle can be drawn

Examiner Tips and Tricks

Always draw a sketch to see which quadrant the complex number is in.

Worked Example

(a) Find the modulus and argument of $z = 2 + 3 i$ , giving your answers correct to 3 significant figures.

Sketch this on an Argand diagram
Form a right-angled triangle

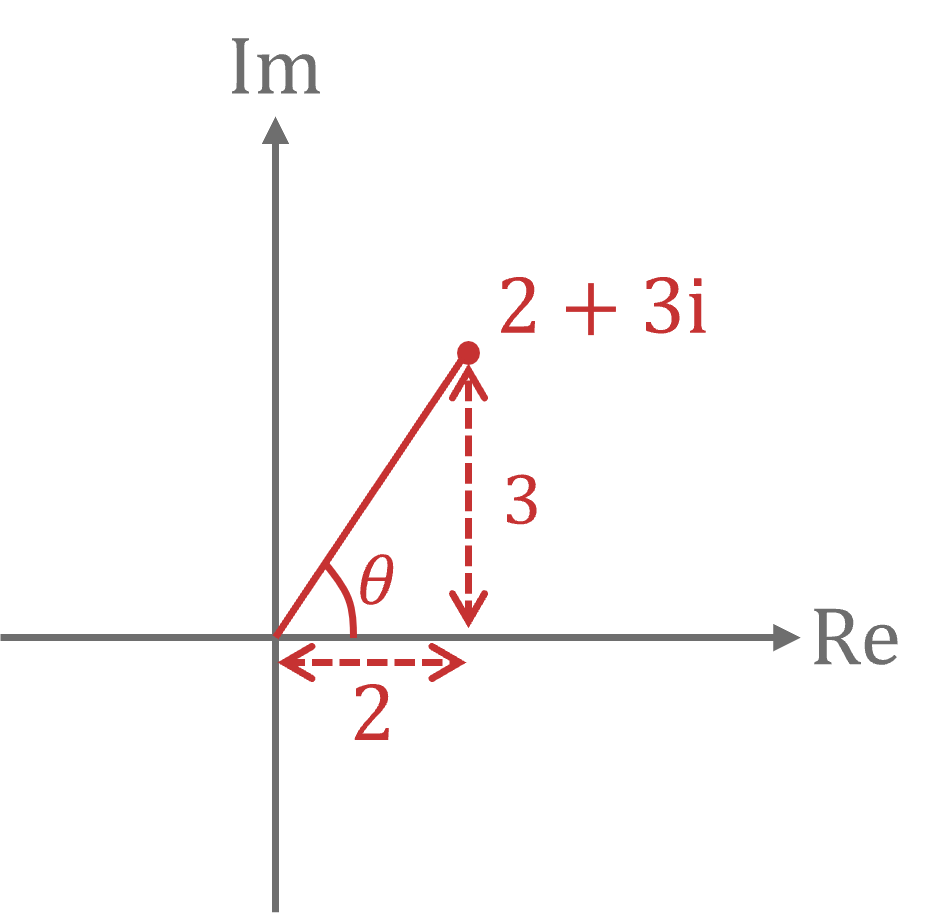
The complex number 2 + 3i on an Argand diagram

Use $|z| = \sqrt{x^{2} + y^{2}}$ (or Pythagoras) to find the modulus

$\begin{array}{rcl} | z | & = & \sqrt{2^{2} + 3^{2}} \\ = & \sqrt{13} \\ = & 3.60555127 . . . \end{array}$

$z$ is in the first quadrant so the argument is positive and acute
Use trigonometry to find the argument $θ$ in radians

$\begin{array}{rcl} \tan θ & = & \frac{3}{2} \\ θ & = & \tan^{- 1} (\frac{3}{2}) \\ θ & = & 0.98279372 . . . \end{array}$

Round the answers to 3 significant figures

$| z | = 3.61$ and $\arg z = 0.983$ to 3 significant figures

(b) Find the modulus and argument of $w = - 1 - \sqrt{3} i$ , leaving your answers as exact values.

Sketch this on an Argand diagram
Form a right-angled triangle

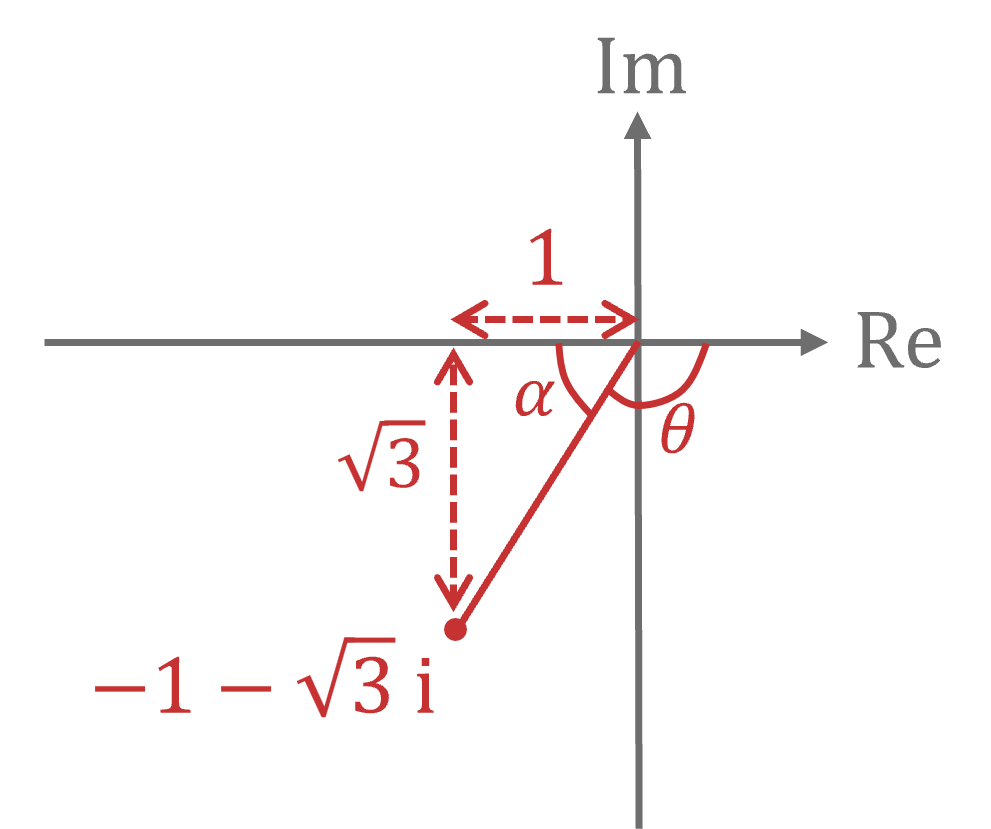
A complex number in the third quadrant on an Argand diagram

Use $|z| = \sqrt{x^{2} + y^{2}}$ (or Pythagoras) to find the modulus

$\begin{array}{rcl} | z | & = & \sqrt{{(- 1)}^{2} + {(- \sqrt{3})}^{2}} \\ = & \sqrt{4} \\ = & 2 \end{array}$

$z$ is in the third quadrant so the argument is negative and obtuse
Use trigonometry to first find $α$ in radians

$\begin{array}{rcl} \tan α & = & \frac{\sqrt{3}}{1} \\ α & = & \tan^{- 1} (\sqrt{3}) \\ α & = & \frac{π}{3} \end{array}$

Then find $θ$ by subtracting $α$ from 180° ( $π$ radians)

$\begin{array}{rcl} θ & = & π - α \\ = & π - \frac{π}{3} \\ = & \frac{2 π}{3} \end{array}$

Remember that the argument here must be a negative angle

$| z | = 2$ and $\arg z = - \frac{2 π}{3}$

These answers must be exact

Modulus-Argument Form

What is modulus-argument form?

All complex numbers can be written in the form:
- $z = r (\cos θ + isin θ)$
- where $r = | z |$ and $θ = \arg z$
  - This is called the modulus-argument (or polar) form
Negative arguments should be shown clearly without simplifying
- $z = 2 (\cos (- \frac{π}{3}) + isin (- \frac{π}{3}))$
  - Simplifying them gives the Cartesian form
  - $z = 2 (\frac{1}{2} + i (- \frac{\sqrt{3}}{2})) = 1 - \sqrt{3} i$
Be careful: $z = r (\cos θ - isin θ)$ is not in modulus-argument form (due to the minus sign)
- Rewrite it as $z = r (\cos (- θ) + isin (- θ))$
  - This uses the symmetries $\cos (- θ) \equiv \cos (θ)$ and $\sin (- θ) \equiv - \sin θ$
- The argument is $- θ$

Worked Example

Write $z = - 4 + 4 i$ in the exact form $r (\cos θ + i \sin θ)$ where $r > 0$ and $- π < θ \leq π$ .

Draw a sketch to find the modulus, $r$ , and argument, $θ$ , of $z$
Form a right-angled triangle

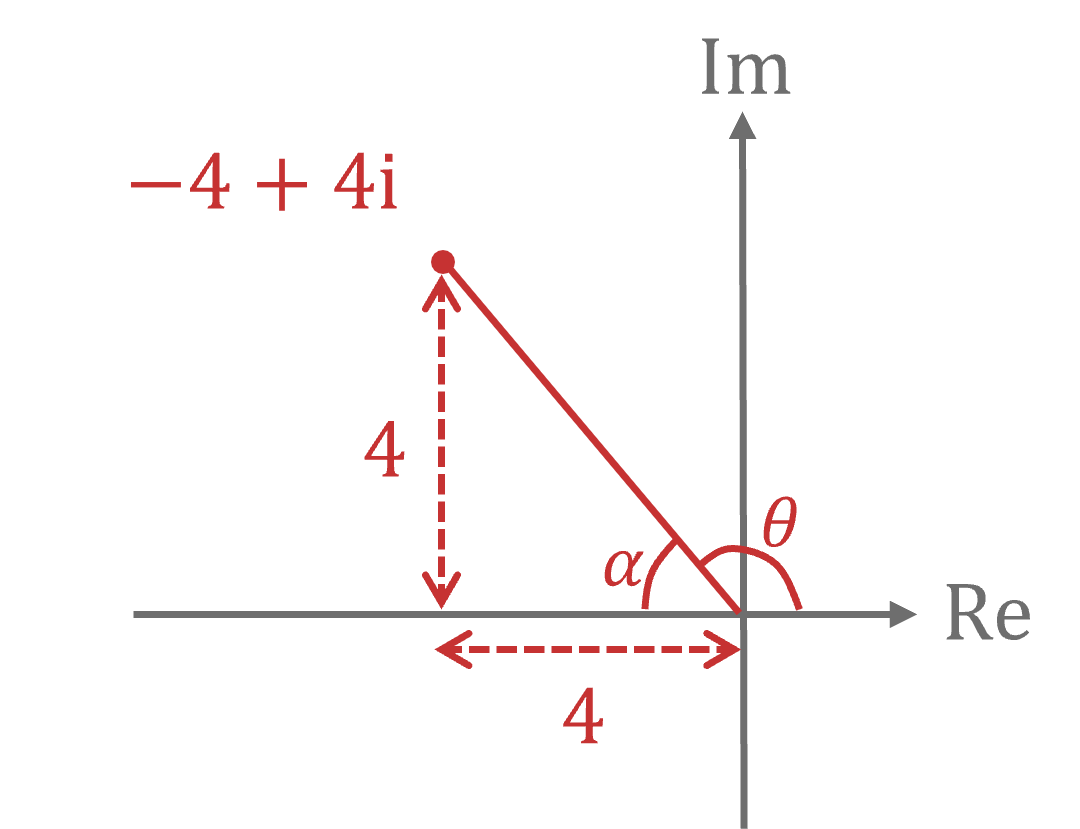
The complex number -4+4i on an Argand diagram

Use $|z| = \sqrt{x^{2} + y^{2}}$ (or Pythagoras) to find the modulus

$\begin{array}{rcl} | z | & = & \sqrt{{(- 4)}^{2} + {(4)}^{2}} \\ = & \sqrt{32} \\ = & 4 \sqrt{2} \end{array}$

$z$ is in the second quadrant so the argument is positive and obtuse
Use trigonometry to first find $α$ in radians

$\begin{array}{rcl} \tan α & = & \frac{4}{4} \\ α & = & \tan^{- 1} (1) \\ α & = & \frac{π}{4} \end{array}$

Then find $θ$ by subtracting $α$ from 180° ( $π$ radians)

$\begin{array}{rcl} θ & = & π - α \\ = & π - \frac{π}{4} \\ = & \frac{3 π}{4} \end{array}$

Write the final answer in the form $r (\cos θ + i \sin θ)$

$z = 4 \sqrt{2} (\cos (\frac{3 π}{4}) + i \sin (\frac{3 π}{4}))$

Leave the modulus and argument exact

Last updated: 10 April 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?

Modulus & Argument (Edexcel International A Level Further Maths)

Revision Note

Argand Diagrams

What is an Argand diagram?

Examiner Tips and Tricks

Worked Example

Modulus & Argument

How do I find the modulus of a complex number?

What rules does the modulus follow?

How do I find the argument of a complex number?

Examiner Tips and Tricks

Worked Example

Modulus-Argument Form

What is modulus-argument form?

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Mark Curtis

Author: Dan Finlay