Born-Haber Calculations (Oxford AQA International A Level (IAL) Chemistry): Revision Note
Exam code: 9622
Born-Haber Calculations
Once a Born-Haber cycle has been constructed, lattice energy (ΔHlattꝋ) can be calculated by applying Hess’s law and rearranging:
ΔHfꝊ = ΔHatꝊ + ΔHatꝊ + ΔHieꝊ+ ΔHeaꝊ + ΔHlattꝊ
If we simplify this into three terms, this makes the equation easier to see:
ΔHlattθ
ΔHfθ
ΔH1θ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
The simplified equation becomes:
ΔHfꝊ = ΔH1Ꝋ + ΔHlattꝊ
So, if we rearrange to calculate the lattice energy, the equation becomes
ΔHlattꝊ = ΔHfꝊ - ΔH1Ꝋ
When calculating the ΔHlattꝊ, all other necessary values will be given in the question
A Born-Haber cycle could be used to calculate any stage in the cycle
For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
Work out the direct and indirect route of the cycle
The stage that you are being asked to calculate will always be the direct route
Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
Remember:
To include all the required enthalpies
Sometimes an enthalpy value may need to be doubled or halved, depending on the ionic solid involved
For example, magnesium chloride
Magnesium has two ionisation energies:
First ionisation energy creating the Mg+ ion
Second ionisation energy creating the Mg2+ ion
There are two chlorine atoms required to form magnesium chloride
Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl- ions
This means that the value for the electron affinity of chlorine is doubled
Worked Example
Using the data below, calculate the ΔHlattθ of magnesium oxide, MgO.
Enthalpy change | Enthalpy change / kJ mol-1 |
|---|---|
ΔHatꝊ Mg | +148 |
ΔHatꝊ O | +248 |
ΔH1ieꝊ Mg | +736 |
ΔH2ieꝊ Mg | +1450 |
ΔH1eaꝊ O | -142 |
ΔH2eaꝊ O | +770 |
ΔHfꝊ MgO | -602 |
Answer:
Step 1: The corresponding Born-Haber cycle is:
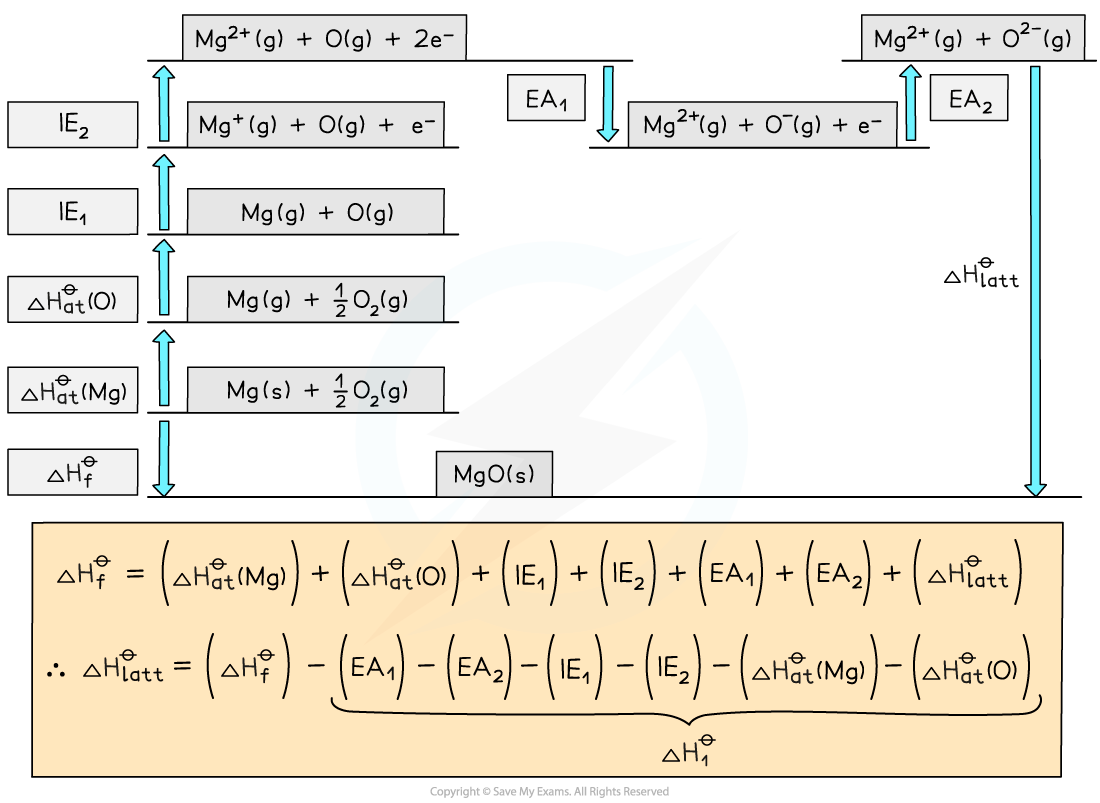
Step 2: Applying Hess’ law, the lattice energy of MgO is:
ΔHlattꝊ = ΔHfꝊ - ΔH1Ꝋ
ΔHlattꝊ = ΔHfꝊ - [( ΔHatꝊ Mg) + (ΔHatꝊ O) + (ΔH1ieꝊ Mg) + (ΔH2ieꝊ Mg) + (ΔH1eaꝊ O) + (ΔH2eaꝊ O)]
Step 3: Substitute in the numbers:
ΔHlattꝊ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
ΔHlattꝊ = -3812 kJ mol-1
Worked Example
Using the data below, calculate the ΔHlattꝊ of potassium chloride, KCl.
Enthalpy change | Enthalpy change / kJ mol-1 |
|---|---|
ΔHatꝊ K | +90 |
ΔHatꝊ Cl | +122 |
ΔHieꝊ K | +418 |
ΔHeaꝊ Cl | -349 |
ΔHfꝊ KCl | -437 |
Answer:
Step 1: The corresponding Born-Haber cycle is:
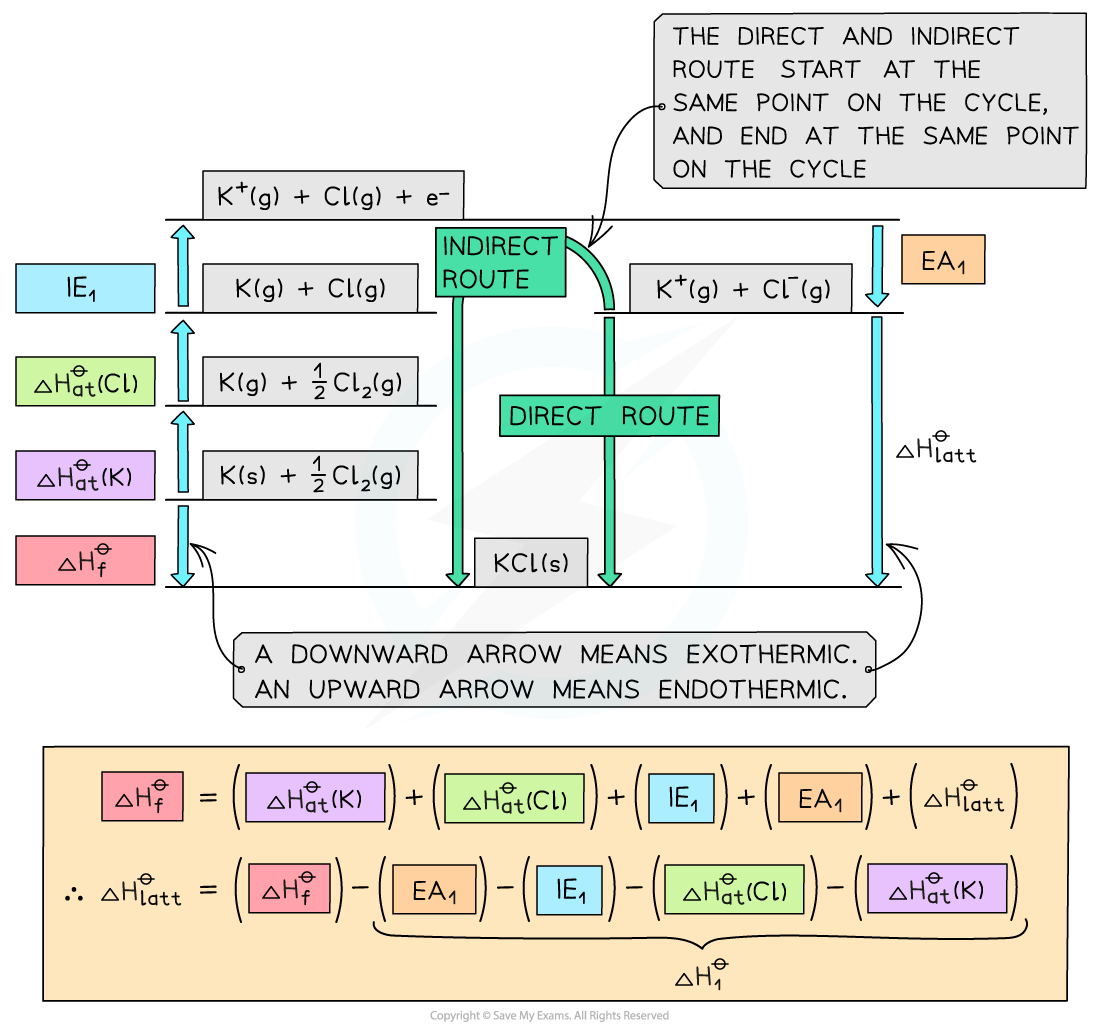
Step 2: Applying Hess’ law, the lattice energy of KCl is:
ΔHlattꝊ = ΔHfꝊ - ΔH1Ꝋ
ΔHlattꝊ = ΔHfꝊ - [(ΔHatꝊ K) + (ΔHatꝊ Cl) + (ΔHieꝊ K) + (ΔHeaꝊ Cl)]
Step 3: Substitute in the numbers:
ΔHlattꝊ = (-437) - [(+90) + (+122) + (+418) + (-349)] = –718 kJ mol-1
Comparing Lattice Enthalpies
It is possible to calculate a theoretical value for the lattice enthalpy of an ionic solid
To do this you need to know:
The geometry of the ionic solid
The charge on the ions
The distance between the ions
Ionic lattice of sodium chloride

This has been calculated for a number of ionic solids and allows a comparison between theoretical lattice enthalpies and experimental lattice enthalpies obtained from Born-Haber cycles
The calculation of the theoretical value assumes that the substance is a highly ionic compound with only electrostatic attraction between cations and anions
Table comparing theoretical and experimental lattice enthalpies
Substance | Theoretical lattice enthalpy / kJ mol-1 | Experimental lattice enthalpy / kJ mol-1 | % difference |
|---|---|---|---|
NaCl | 769 | 790 | 2.7 |
ZnS | 3427 | 3615 | 5.5 |
You can see from the table that there is quite close agreement between the two values for the lattice enthalpy of sodium chloride
The difference between theoretical and experimental lattice enthalpy increases for zinc sulfide
This suggests that the bonding is not purely ionic and some covalent character is present
This can be explained as follows:
Zn2+ is a smaller ion with a greater charge than Na+
Zn2+ ions attract electron density towards themselves
This distorts the electron cloud and makes the bonding slightly covalent
S2- ions are larger ions than chloride ions Cl- with a greater negative charge
The electron cloud around S2- is more easily distorted than in chloride ions leading to further covalent character
Distortion of electron clouds
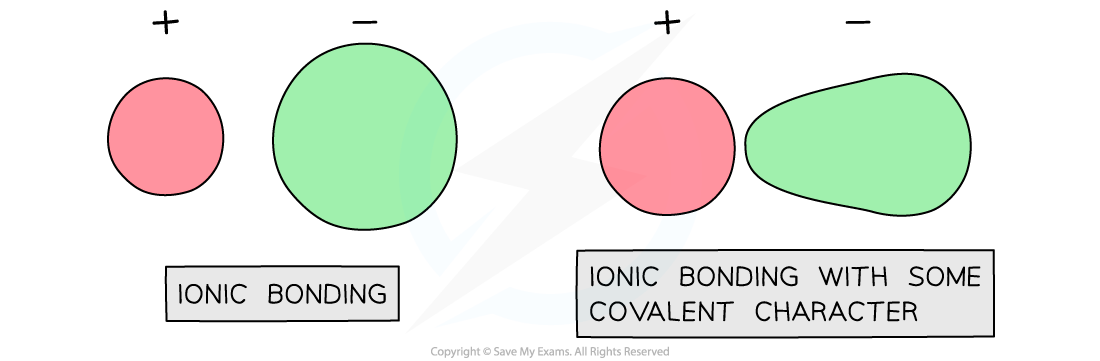
As you move left to right across the period table, the lattices become less ionic and more covalent leading to a discrepancy in the lattice enthalpy values
The result of these analyses provides strong evidence that supports the ionic model for some compounds like sodium chloride

Unlock more, it's free!
Did this page help you?