The Arrhenius Equation (Oxford AQA International A Level (IAL) Chemistry): Revision Note
Exam code: 9622
The Arrhenius Equation
The rate equation shows how each reactant affects the rate of the reaction
It includes the rate constant, k
However, k only remains constant if the concentration of the reactants is the only factor which is changed
If the temperature is changed or a catalyst is used or changed, then the rate constant, k, changes
At higher temperatures, a greater proportion of molecules have energy greater than the activation energy
Since the rate constant and rate of reaction are directly proportional to the fraction of molecules with energy equal or greater than the activation energy, then at higher temperatures:
The rate of reaction increases
The rate constant increases
The relationship between the rate constant, the temperature and also the activation energy is given by the Arrhenius equation:
Terms in the Arrhenius Equation:
Ea and A are constants that are characteristic of a specific reaction
A does vary slightly with temperature but it can still be considered a constant
R is a fundamental physical constant for all reactions
k and T are the only variables in the Arrhenius equation
The Arrhenius equation is used to describe reactions that involve:
Gases
Reactions that occur in solution
Reactions that occur on the surface of a catalyst
Activation Energy Calculations
The Arrhenius Equation is often used to calculate:
The activation energy, Ea, of a reaction
The Arrhenius constant, A, for a reaction
A question will give sufficient information for:
The Arrhenius equation to be used
Or, a graph to be plotted and the calculation done from the plot
Using the Arrhenius equation
The Arrhenius equation is easier to use if you take natural logarithms of each side of the equation, which results in the following equation:
How temperature affects the rate constant and rate of reaction:
An increase in temperature gives a greater value of ln k
This results in a higher value for the rate constant, k
Since the rate of the reaction depends on the rate constant, k, an increase in k also means an increased rate of reaction
How activation energy affects the rate constant:
An increase in the activation energy, Ea, means a smaller proportion of molecules has the required activation energy
This results in a lower value for the rate constant, k
Since the rate of the reaction depends on the rate constant, k, a decrease in k also means a decreased rate of reaction
The values of k and T for a reaction can be determined experimentally
These values of k and T can then be used to calculate the activation energy for a reaction
This is the most common type of calculation you will be asked to do on this topic
Examiner Tips and Tricks
In the exam, you could be asked to calculate any part of the Arrhenius Equation. Using the equation in its natural logarithm form makes this easier.
Worked Example
Calculate the activation energy of a reaction which takes place at 400 K, where the rate constant of the reaction is 6.25 x 10-4 s-1.
A = 4.6 x 1013 and R = 8.31 J K-1 mol-1.
Answer:
Rearrange the equation for Ea:
Insert the values from the question:
Ea = 129095.85 J
Convert from J to kJ:
Ea = 129 kJ
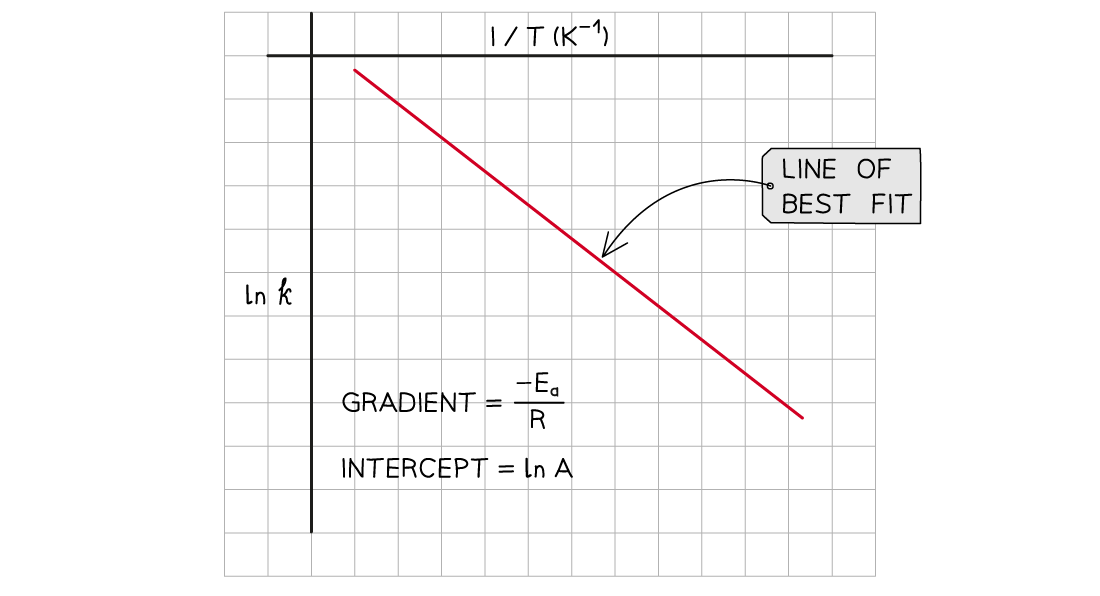
Using an Arrhenius plot
A graph of ln k against 1/T can be plotted, and then used to calculate Ea
This gives a line which follows the form y = mx + c
Where:
y = ln k
x =
m =
(the gradient)
c = ln A (the y-intercept)
The equation shows that an increase in temperature (higher value of T) gives a greater value of ln k (and therefore a higher value of k)
Since the rate of the reaction depends on the rate constant (k) an increase in k also means an increased rate of reaction
Example graph of ln k over 1/T
Worked Example
Complete the following table.
Temperature | 1/T | Time, t | Rate constant, k | ln k |
|---|---|---|---|---|
310 | 3.23 x 10-3 | 57 | -9.2 | |
335 | 31 | 3.01 x 10-4 | -8.1 | |
360 | 2.78 x 10-3 | 19 | 5.37 x 10-4 | -7.5 |
385 | 2.60 x 10-3 | 7 | 9.12 x 10-4 |
Plot a graph of ln k against 1/T.
Using the graph and following equation, calculate the activation energy, Ea, for this reaction.
Calculate the Arrhenius constant, A, for this reaction.
Answers:
The completed table is:
Temperature | 1/T | Time, t | Rate constant, k | ln k |
|---|---|---|---|---|
310 | 3.23 x 10-3 | 57 | 1.01 x 10-4 | -9.2 |
335 | 2.99 x 10-3 | 31 | 3.01 x 10-4 | -8.1 |
360 | 2.78 x 10-3 | 19 | 5.37 x 10-4 | -7.5 |
385 | 2.60 x 10-3 | 7 | 9.12 x 10-4 | -7.0 |
The graph of ln k against 1/T is:
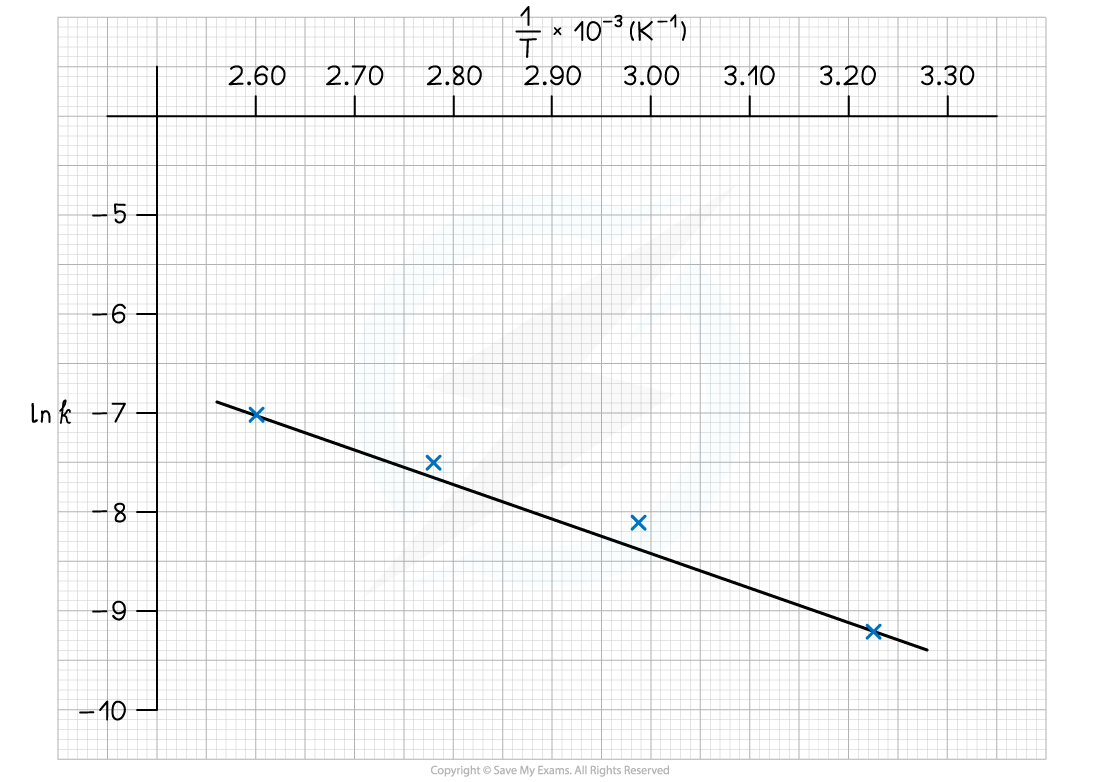
To calculate the activation energy, Ea:

Gradient = -Ea / R = -3666.6
Ea = -(-3666.6 x 8.31) = 30, 469 J mol-1
Ea = -(-3666.6 x 8.31) = 30.5 kJ mol-1
To calculate the Arrhenius constant, A:
Choose a point on the graph, e.g (2.60 x 10-3, -7.0)

Substitute values into the equation
-7.0 = (-3666.6 x 2.60 x 10-3) + ln A
-7.0 = -9.53 + ln A
ln A = 2.53
A =
A = 12.55
Examiner Tips and Tricks
You are not required to learn these equations. However, you do need to be able to rearrange them, and knowing them is helpful in understanding the effects of temperature on the rate constant.

Unlock more, it's free!
Was this revision note helpful?
