Determination of Rate Equation (Oxford AQA International A Level Chemistry)

Concentration-Time Graphs

Using concentration–time graphs

• Concentration–time graphs can be used to deduce:

  • The overall rate of a reaction

  • The order with respect to an individual reactant

• In a zero-order reaction, the concentration of the reactant is inversely proportional to time

  • This means that the concentration of the reactant decreases with increasing time

  • The graph is a straight line going down

• In a first-order reaction, the concentration of the reactant decreases with time

  • The graph is a curve going downwards and eventually plateaus

• In a second-order reaction, the concentration of the reactant decreases more steeply with time

  • The concentration of reactant decreases more with increasing time compared to in a first-order reaction

  • The graph is a steeper curve going downwards

Using initial concentration–time data

• Initial concentration–time data can be used to deduce the initial rate of a reaction

  • The initial rate of a reaction is the rate right at the start of the reaction

  • This is used because right at the start of the reaction, we know the exact concentration of the reactants used

• To calculate the initial rate of reaction:

  • Draw a tangent to the curve at time, t = 0 s

  • Calculate the gradient of the tangent line

• One alternative to this gathers experimental data to determine the order with respect to the reactants in the reaction

• The method involves setting up a series of experiments

• When carrying out the experiments:

  • The temperature must remain constant

  • For each experiment, the concentration of only one reactant is altered

    • The remaining reactant concentrations remain constant

  • The experiments are planned so that when the results are collected, they can be used to determine the order with respect to each reactant

  • For each experiment, a concentration-time graph is drawn

  • From each graph, the initial rate is calculated by drawing a tangent to the line at t = 0 and calculating the gradient

  • The gradient at t = 0 is the initial rate for that reaction

General Example

• Let's take the following general reaction as an example

2A + B + C → C + D

• We need to run a series of experiments at different concentrations of A, B and C, to determine how each affects the initial rate of the reaction

  • Experiment 1 - use the same concentrations of A, B and C

  • Experiment 2 - change the concentration of A but keep the concentrations of B and C the same as in experiment 1

  • Experiment 3 - change the concentration of B but keep the concentrations of A and C the same as in experiment 1

  • Experiment 4 - change the concentration of C but keep the concentrations of A and B the same as in experiment 1

• Plot graphs for each experiment

• Draw a tangent at t=0 and calculate the gradient (the initial rate) for each graph

• Record the concentrations and initial rates of reaction in a suitable table

• Use these results to determine the order with respect to each reactant

  • Order with respect to [A]:

    • Use experiments 1 and 2

    • [A] doubles

    • No effect on the intial rate

    • Therefore, the reaction is zero order with respect to [A]

  • Order with respect to [B]:

    • Use experiments 1 and 3

    • [B] doubles

    • The intial rate doubles

    • Therefore, the reaction is first order with respect to [B]

  • Order with respect to [C]:

    • Use experiments 1 and 4

    • [C] doubles

    • The initial rate increases by a factor of 4

    • Therefore, the reaction is second order with respect to [C]

• Use the orders, to write the rate equation for the reaction:

  • Rate = k [B] [C]²

Using rate-concentration graphs

• The progress of the reaction can be followed by measuring the initial rates of the reaction using various initial concentrations of each reactant

• These rates can then be plotted against time in a rate-time graph

• In a zero-order reaction, the rate does not depend on the concentration of the reactant

  • The rate of the reaction therefore remains constant throughout the reaction

  • The graph is a horizontal line

  • The rate equation is rate = k 

• In a first-order reaction, the rate is directly proportional to the concentration of a reactant

  • The rate of the reaction decreases as the concentration of the reactant decreases when it gets used up during the reaction

  • The graph is a straight line

  • The rate equation is rate = k [A] 

• In a second-order reaction, the rate is directly proportional to the square of concentration of a reactant

  • The rate of the reaction decreases more as the concentration of the reactant decreases when it gets used up during the reaction

  • The graph is a curved line

  • The rate equation is rate = k [A]² 

Rates & Reaction Mechanisms

• The reaction mechanism of a reaction describes how many steps are involved in the making and breaking of bonds during a chemical reaction

• It is the slowest step in a reaction and includes the reactants that have an impact on the reaction rate when their concentrations are changed

  • Therefore, all reactants that appear in the rate equation will also appear in the rate-determining step

  • This means that zero-order reactants and intermediates will not be present in the rate-determining step

Predicting the reaction mechanism

• The overall reaction equation and rate equation can be used to predict a possible reaction mechanism of a reaction

• For example, nitrogen dioxide (NO₂) and carbon monoxide (CO) react to form nitrogen monoxide (NO) and carbon dioxide (CO₂)

• The overall reaction equation is:

NO₂ (g) + CO (g) → NO (g) + CO₂ (g)

• The rate equation is:

Rate = k [NO₂]²

• From the rate equation, it can be concluded that the reaction is zero order with respect to CO (g) and second order with respect to NO₂ (g)

• This means that there are two molecules of NO₂ (g) involved in the rate-determining step

• A possible reaction mechanism could therefore be:

  • Step 1:

    • 2NO₂ (g) → NO (g) + NO₃ (g)     slow (rate-determining step)

  • Step 2:

    • NO₃ (g) + CO (g) → NO₂ (g) + CO₂ (g)     fast

  • Overall:

    • 2NO₂ (g) + NO₃ (g) + CO (g) → NO (g) + NO₃ (g) + NO₂ (g) + CO₂ (g)

    • Which simplifies to NO₂ (g) + CO (g) → NO (g) + CO₂ (g)

Predicting the reaction order & deducing the rate equation

• The order of a reactant and thus the rate equation can be deduced from a reaction mechanism given that the rate-determining step is known

• For example, the reaction of nitrogen oxide (NO) with hydrogen (H₂) to form nitrogen (N₂) and water

2NO (g) + 2H₂ (g) → N₂ (g) + 2H₂O (l)

• The reaction mechanism for this reaction is:

  • Step 1:

    • NO (g) + NO (g) → N₂O₂ (g)     fast

  • Step 2:

    • N₂O₂ (g) + H₂ (g) → H₂O (l) + N₂O (g)     slow (rate-determining step)

  • Step 3:

    • N₂O (g) + H₂ (g) → N₂ (g) + H₂O (l)     fast

  • The second step in this reaction mechanism is the rate-determining step

  • The rate-determining step consists of:

    • N₂O₂ which is formed from the reaction of two NO molecules

    • One H₂ molecule

• The reaction is, therefore, second order with respect to NO and first order with respect to H₂

  • So, the rate equation becomes:

Rate = k [NO]² [H₂]

• The reaction is, therefore, third-order overall

Identifying the rate-determining step

• The rate-determining step can be identified from a rate equation given that the reaction mechanism is known

• For example, propane (CH₃CH₂CH₃) undergoes bromination under alkaline solutions

• The overall reaction is:

CH₃CH₂CH₃ + Br₂ + OH^- → CH₃CH₂CH₂Br + H₂O + Br^-

• The reaction mechanism is:

• The rate equation is:

Rate = k [CH₃CH₂CH₃] [OH^-]

• From the rate equation, it can be deduced that only CH₃COCH₃ and OH^- are involved in the rate-determining step and not bromine (Br₂)

• CH₃COCH₃ and OH^- are only involved in step 1

  • Therefore, the rate-determining step is step 1 of the reaction mechanism

Identifying intermediates & catalyst

• When a rate equation includes a species that is not part of the chemical reaction equation then this species is a catalyst

• For example, the halogenation of butanone under acidic conditions

• The reaction mechanism is:

CH₃CH₂COCH₃ + I₂  CH₃CH₂COCH₂I + HI

• The reaction mechanism is:

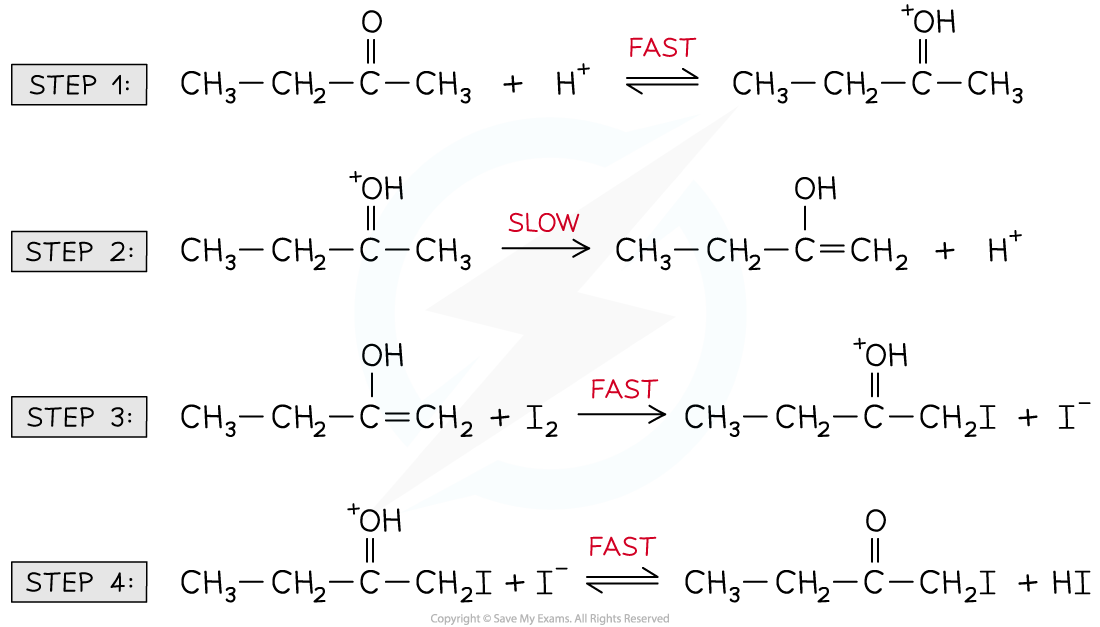
• The rate equation is:

Rate = k [CH₃CH₂COCH₃] [H⁺]

• The H⁺ is not present in the chemical reaction equation but does appear in the rate equation

  • H⁺ must therefore be a catalyst

• Furthermore, the rate equation suggests that CH₃CH₂COCH₃ and H⁺ must be involved in the rate-determining (slowest) step

• The CH₃CH₂COCH₃ and H⁺ appear in the rate-determining step in the form of an intermediate (which is a combination of the two species)