Kp Calculations (Oxford AQA International A Level Chemistry)

Revision Note

Written by: Richard Boole

Reviewed by: Stewart Hird

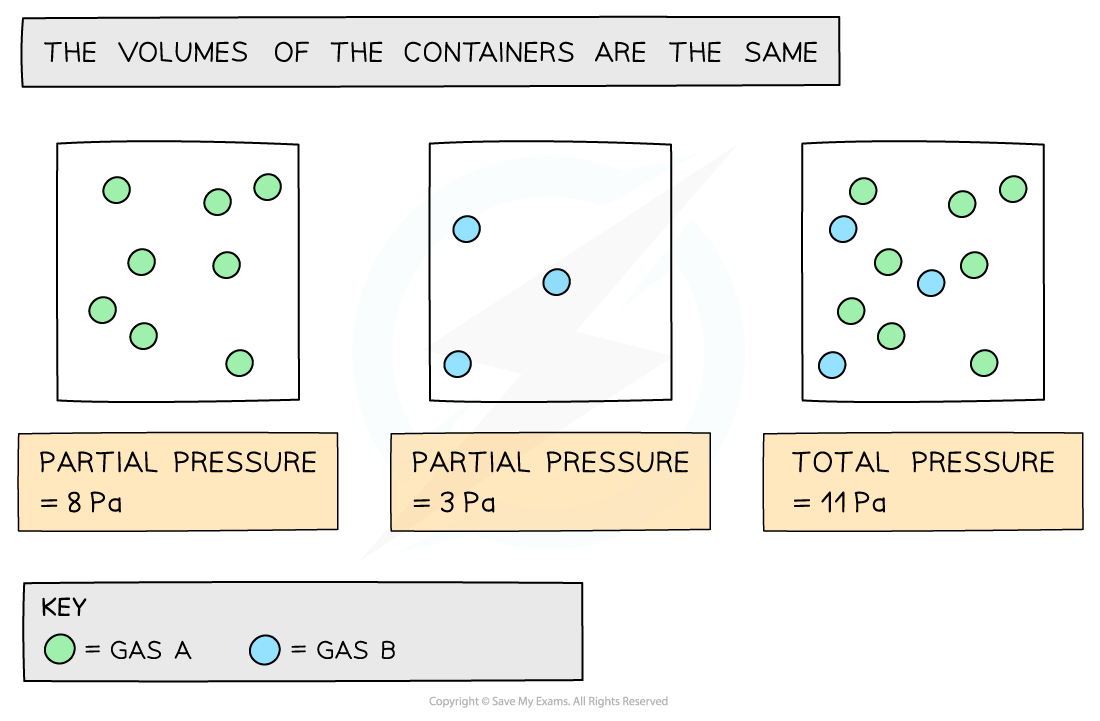
Partial Pressure

For reactions involving mixtures of gases, the equilibrium constant K_p is used
- This is because it is easier to measure the pressure than the concentration for gases
The partial pressure of a gas is the pressure that the gas would have if it was in the container all by itself
The total pressure is the sum of all the partial pressures:

P_total = P_A + P_B + P_C + .......

Where:
- P_total = total pressure
- P_A, P_B, P_C = partial pressures

How partial pressures contribute to total pressure

Equilibria Partial Pressures — **Partial pressures can be added together to calculate the total pressure**

Mole fraction

The mole fraction of a gas is the ratio of moles of a particular gas to the total number of moles of gas present

$Mole fraction = \frac{number of moles of a particular gas}{total number of moles of all the gases in the mixture}$

This equation can be used to calculate the partial pressure of each gas:

$Partial pressure = mole fraction \times total pressure$

Examiner Tips and Tricks

You can check that your mole fractions and partial pressures are correct:

The sum of the mole fractions should add up to 1
The sum of the partial pressures should add up to the total pressure

Worked Example

A sample of 0.25 mole of nitrogen and 0.75 mole of hydrogen were reacted together to form ammonia. The equilibrium amount of nitrogen was 0.16 mole at a pressure of 75 kPa.

N₂(g) + 3H₂ (g) ⇌ 2NH₃(g)

Calculate the mole fractions of nitrogen, hydrogen and ammonia.
Calculate the partial pressures of nitrogen, hydrogen and ammonia.

Answer:

The mole fractions of nitrogen, hydrogen and ammonia:
- Complete an ICE table:
  N₂ (g)
  3H₂ (g)
  2NH₃ (g)
  Initial
  0.25 mol
  0.75 mol
  0.00 mol
  Change
  0.25 - 0.16
  = -0.09
  -3 x 0.09
  = -0.27
  +2 x 0.09
  = +0.18
  Equilibrium
  0.16 mol
  0.75 - 0.27
  = 0.48 mol
  0.18 mol
- Calculate the total number of moles:
  - 0.16 + 0.48 + 0.18 = 0.82
- Calculate the mole fractions:
  - N₂ (g) = 0.16 / 0.82 = 0.195
  - H₂ (g) = 0.48 / 0.82 = 0.585
  - NH₃ (g) = 0.18 / 0.82 = 0.220
The partial pressures of nitrogen, hydrogen and ammonia:
- Partial pressure = mole fraction x total pressure
  - N₂ (g) = 0.195 x 75 = 14.625 kPa
  - H₂ (g) = 0.585 x 75 = 43.875 kPa
  - NH₃ (g) = 0.220 x 75 = 16.5 kPa

	N₂ (g)	3H₂ (g)	2NH₃ (g)
Initial	0.25 mol	0.75 mol	0.00 mol
Change	0.25 - 0.16 = -0.09	-3 x 0.09 = -0.27	+2 x 0.09 = +0.18
Equilibrium	0.16 mol	0.75 - 0.27 = 0.48 mol	0.18 mol

K_p Calculations

K_pcalculations are a step-by-step process
Some questions may give the equilibrium partial pressure of all the gases
This means that the only remaining steps are:
- Write the K_pexpression
- Calculate the value of K_p

Worked Example

The equilibrium between sulfur dioxide, oxygen and sulfur trioxide is as follows:

2SO₂ (g) + O₂ (g) $⇌$ 2SO₃ (g)

At constant temperature, the equilibrium partial pressures are:

SO₂ = 1.0 x 10⁶ Pa
O₂ = 7.0 x 10⁶ Pa
SO₃ = 8.0 x 10⁶ Pa

Calculate the value of K_p for this reaction.

Answer:

Step 1: Write the equilibrium constant for the reaction in terms of partial pressures:
- K_p = $\frac{p^{2} {SO}_{3}}{p^{2} {SO}_{2} \times p O_{2}}$

Step 2: Substitute the equilibrium concentrations into the expression:
- K_p = $\frac{{(8.0 \times 10^{6})}^{2}}{{(1.0 \times 10^{6})}^{2} \times (7.0 \times 10^{6})}$
- K_p = 9.1 x 10^–6

Step 3: Deduce the correct units of K_p:
- K_p = $\frac{{Pa}^{2}}{{Pa}^{2} \times Pa}$
- So, the units of K_p are Pa^-1
- Therefore, K_p = 9.1 x 10^-6 Pa^-1

Some questions give the number of moles of gases present and the total pressure
So, the steps to complete these problems are:
- Calculate the mole fractions
- Calculate the partial pressures
- Write the K_pexpression
- Calculate the value of K_p

Worked Example

The equilibrium between hydrogen, iodine and hydrogen iodide is as follows:

H₂ (g) + I₂ (g) $⇌$ 2HI (g)

At constant temperature, the equilibrium moles are:

H₂ = 1.71 x 10^–3
I₂ = 2.91 x 10^–3
HI = 1.65 x 10^–2

The total pressure is 100 kPa.

Calculate the value of K_p for this reaction.

Answer:

Step 1: Calculate the total number of moles:
- Total number of moles = 1.71 x 10^-3+ 2.91 x 10^-3+ 1.65 x 10^-2
- Total number of moles = 2.112 x 10^-2

Step 2: Calculate the mole fraction of each gas:
- H₂ = $\frac{1.71 \times 10^{- 3}}{2.112 \times 10^{- 2}}$ = 0.0810
- I₂ = $\frac{2.91 \times 10^{- 3}}{2.112 \times 10^{- 2}}$ = 0.1378
- HI = $\frac{1.65 \times 10^{- 2}}{2.112 \times 10^{- 2}}$ = 0.7813

Step 3: Calculate the partial pressure of each gas:
- H₂ = 0.0810 x 100 = 8.10 kPa
- I₂ = 0.1378 x 100 = 13.78 kPa
- HI = 0.7813 x 100 = 78.13 kPa

Step 4: Write the equilibrium constant in terms of partial pressure:
- K_p = $\frac{p^{2} HI}{p H_{2} \times p I_{2}}$

Step 5: Substitute the values into the equilibrium expression:
- K_p = $\frac{78 . 13^{2}}{8.10 \times 13.78}$
- K_p = 54.7

Step 6: Deduce the correct units for K_p:
- K_p = $\frac{{Pa}^{2}}{Pa \times Pa}$
- All units cancel out
- Therefore, K_p = 54.7

A full K_p question will give:
- Initial number of moles of the gases present
- The equilibrium number of moles of at least one of the gases present
- The total pressure
So, the steps to complete these problems are:
- Determine the number of equilibrium moles of all gases
- Calculate the mole fractions
- Calculate the partial pressures
- Write the K_pexpression
- Calculate the value of K_p

Worked Example

Hydrogen and bromine were mixed in a flask in a 1 : 1 ratio and allowed to reach equilibrium at 450 K. When equilibrium had been achieved the total pressure in the flask was 140 kPa and the mole fraction of bromine was 0.35.

The equation for the reaction is:

H₂ (g) + Br₂ (g) ⇌ 2HBr (g)

Determine the partial pressures for each gas at equilibrium and the value of K_p.

Answer:

H₂ and Br₂are in a 1 : 1 ratio
- So, the mole fraction of Br₂ = the mole fraction of H₂
- Mole fraction of hydrogen = 0.35
The mole fraction of hydrogen bromide is the remainder of the mole fraction
- This is because the total mole fraction adds up to 1
- So, the mole fraction of HBr = 1 - the mole fraction of H₂ - the mole fraction of Br₂
- Mole fraction of hydrogen bromide = 1 - 0.35 - 0.35 = 0.3
The partial pressures are calculated by mole fraction x total pressure:
- Partial pressure H₂ = 0.35 x 140 = 49 kPa
- Partial pressure Br₂ = 0.35 x 140 = 49 kPa
- Partial pressure HBr = 0.30 x 140 = 42 kPa
The K_p expression is:
- K_p = $\frac{p^{2} HBr (g)}{p H_{2} (g) \times p {Br}_{2} (g)}$
The value of K_p is:
- K_p = $\frac{42^{2}}{49 \times 49}$ = 0.735
There are no units for this K_p value
- The kPa² term on top is cancelled by the kPa x kPa on the bottom

Examiner Tips and Tricks

You need to be able to start from initial moles to calculate equilibrium moles and continue to calculate K_p values.

You also need to be able to work backwards to deduce partial pressures and equilibrium moles from given information.

Last updated: 13 May 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?

Kp Calculations (Oxford AQA International A Level Chemistry)

Revision Note

Partial Pressure

How partial pressures contribute to total pressure

Mole fraction

Examiner Tips and Tricks

Worked Example

K_p Calculations

Worked Example

Worked Example

Worked Example

Examiner Tips and Tricks

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Richard Boole

Author: Stewart Hird