Weak Acids & Bases; Ka for Weak Acids (Oxford AQA International A Level Chemistry)
Revision Note
Written by: Alexandra Brennan
Reviewed by: Stewart Hird
Acid Dissociation Constant, Ka
Weak acids
A weak acid is an acid that partially (or incompletely) dissociates in aqueous solutions
Eg. most organic acids (ethanoic acid), HCN (hydrocyanic acid), H2S (hydrogen sulfide) and H2CO3 (carbonic acid)
The position of the equilibrium is more over to the left and an equilibrium is established
As this is an equilibrium we can write an equilibrium constant expression for the reaction
This constant is called the dissociation constant for a weak acid, Ka, and has the units mol dm-3
Values of Ka are very small, for example for ethanoic acid Ka = 1.74 x 10-5 mol dm-3
When writing the equilibrium expression for weak acids, the following assumptions are made:
The concentration of hydrogen ions due to the ionisation of water is negligible
The value of Ka indicates the extent of dissociation
The higher the value of Ka the more dissociated the acid and the stronger it is
The lower the value of Ka the weaker the acid
Worked Example
Write the expression for the following acids:
Benzoic acid, C6H5COOH
Carbonic acid, H2CO3
Answer:
pKa Calculations
Calculating pH from Ka
The pH of weak acids can be calculated when the following is known:
The concentration of the acid
The Ka value of the acid
From the Ka expression we can see that there are three variables:
However, the equilibrium concentration of [H+] and [A-] will be the same since one molecule of HA dissociates into one of each ion
This means you can simplify and re-arrange the expression to
Ka x [HA] = [H+]2
[H+]2 = Ka x [HA]
Taking the square roots of each side
[H+] = √(Ka x [HA])
Then take the negative logs
pH = -log[H+] = -log√(Ka x [HA])
Worked Example
Calculate the pH of 0.100 mol dm-3 ethanoic acid at 298 k with a Ka value of 1.74 × 10-5 mol dm-3.
Answer:
Ethanoic acid is a weak acid which ionises as follows:
CH3COOH (aq) ⇌ H+ (aq) + CH3COO- (aq)
Step 1: Write down the equilibrium expression to find Ka
Step 2: Simplify the expression
The ratio of H+ to CH3COO- ions is 1:1
The concentration of H+ and CH3COO- ions are therefore the same
The expression can be simplified to:
Step 3: Rearrange the expression to find [H+]
Step 4: Substitute the values into the expression to find [H+]
= 1.32 x 10-3 mol dm-3
Step 5: Find the pH
pH = -log[H+]
= -log(1.32 x 10-3)
= 2.88
Using pKa
The range of values of Ka is very large and for weak acids, the values themselves are very small numbers
Table of Ka values
Acid | Ka / mol dm-3 |
|---|---|
methanoic acid, HCOOH | 1.77 x 10-4 |
ethanoic acid. CH3COOH | 1.74 x 10-5 |
benzoic acid. C6H5COOH | 6.46 x 10-5 |
carbnonic acid, H2CO3 | 4.30 x 10-7 |
For this reason it is easier to work with another term called pKa
The pKa is the negative log of the Ka value, so the concept is analogous to converting [H+] into pH values
pKa = -logKa
Looking at the pKa values for the same acids:
Table of pKa values
Acid | Ka / mol dm-3 | pKa* |
|---|---|---|
methanoic acid, HCOOH | 1.77 x 10-4 | 3.75 |
ethanoic acid. CH3COOH | 1.74 x 10-5 | 4.75 |
benzoic acid. C6H5COOH | 6.46 x 10-5 | 4.18 |
carbnonic acid, H2CO3 | 4.30 x 10-7 | 6.36 |
*The range of pKa values for most weak acids lies between 3 and 7
Worked Example
At 298 K, a solution of 0.100 mol dm-3 ethanoic acid has a hydrogen ion concentration of 1.32 x 10-3 mol dm-3.
Calculate the Ka & pKa of the acid.
Answer:
Step 1: Write down the equation for the partial dissociation of ethanoic acid
CH3COOH (aq) ⇌ H+ (aq) + CH3COO- (aq)
Step 2: Write down the equilibrium expression to find Ka
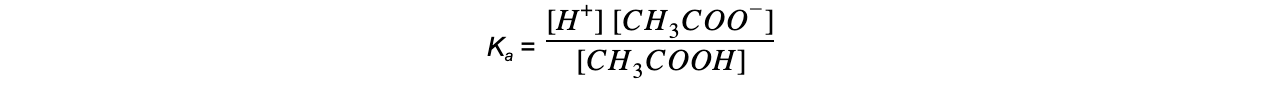
Step 3: Simplify the expression
The ratio of H+ to CH3COO- is 1:1
The concentration of H+ and CH3COO- is, therefore, the same
The equilibrium expression can be simplified to:
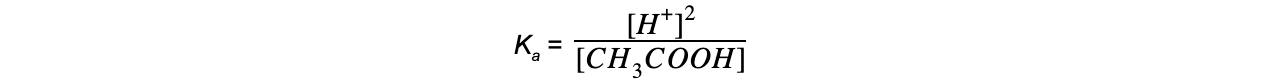
Step 4: Substitute the values into the expression to find Ka
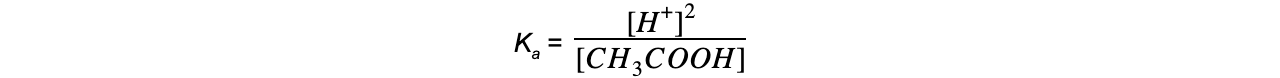
= 1.74 x 10-5
Step 5: Determine the units of Ka
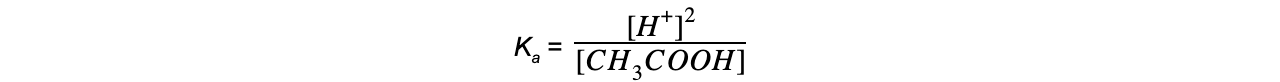
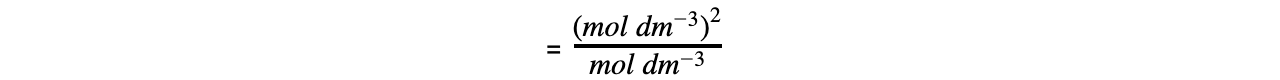
= mol dm-3
The value of Ka is therefore 1.74 x 10-5 mol dm-3
Step 6: Find pKa
pKa = - log10Ka
= - log10 (1.74 x 10-5)
= 4.76
Last updated:
You've read 0 of your 10 free revision notes
Unlock more, it's free!
Did this page help you?
