Born-Haber Cycles (Edexcel International A Level (IAL) Chemistry): Revision Note
Exam code: YCH11
Born-Haber Cycles - Construction
A Born-Haber cycle is a specific application of Hess’ Law for ionic compounds and enable us to calculate lattice enthalpy which cannot be found by experiment
The basic principle of drawing the cycle is to construct a diagram in which energy increases going up the diagram

The basic principle of a Born-Haber cycle
The cycle shows all the steps needed to turn atoms into gaseous ions and from gaseous ions into the ionic lattice
The alternative route to the ionic lattice begins from the enthalpy of formation of the elements in their standard states
Drawing the cycle for sodium chloride
A good starting point is to draw the elements with their state symbols about a third of the way up the diagram
This is shown as the left hand side of the equation for the process indicated
The location is marked by drawing a horizontal bar or line which represents the starting energy level

Drawing a Born-Haber cycle step 1
Next, we need to create the gaseous ions
This is a two step process of first creating the gaseous atoms and then turning them into ions
Creating gaseous atoms is a bond breaking process, so arrows must be drawn upwards
It doesn't matter whether you start with sodium or chlorine
The enthalpy of atomisation of sodium is
Na (s) → Na (g) ΔatHꝋ = +108 kJ mol -1
The enthalpy of atomisation of chlorine is
½Cl2 (g) → Cl (g) ΔatHꝋ = +121 kJ mol -1
We can show the products of the process on the horizontal lines and the energy value against a vertical arrow connecting the energy levels

Drawing a Born-Haber cycle step 2 - creating the gaseous atoms
Now the ions are created
The sodium ion loses an electron, so this energy change is the first ionisation energy for sodium
Na (g) → Na+ (g) + e– ΔieHꝋ = +500 kJ mol-1
The change is endothermic so the direction continues upwards
The chlorine atom gains an electron, so this is electron affinity
Cl (g) + e– → Cl- (g) ΔeaHꝋ = -364 kJ mol-1
The exothermic change means this is downwards
The change is displaced to the right to make the diagram easier to read

Drawing a Born-Haber cycle step 3 - creating the gaseous ions
The two remaining parts of the cycle can now be completed
The enthalpy of formation of sodium chloride is added at the bottom of the diagram
Na (s) + ½Cl2 (g) → NaCl (s) ΔfHꝋ = -411 kJ mol -1
This is an exothermic change for sodium chloride so the arrow points downwards
Enthalpy of formation can be exothermic or endothermic, so you may need to show it above the elements ( and displaced to the right) for a endothermic change
The final change is lattice enthalpy, which is usually shown a formation. For sodium chloride the equation is
Na+(g) + Cl-(g) → NaCl (s) ΔlattHꝋ

Drawing a Born-Haber cycle step 4 - completing the cycle
The cycle is now complete
The cycle is usually used to calculate the lattice enthalpy of an ionic solid, but can be used to find other enthalpy changes if you are given the lattice enthalpy
Worked Example
Constructing a Born-Haber cycle for KCl
Construct a Born-Haber Cycle which can be used to calculate the lattice energy of potassium chloride

Answer
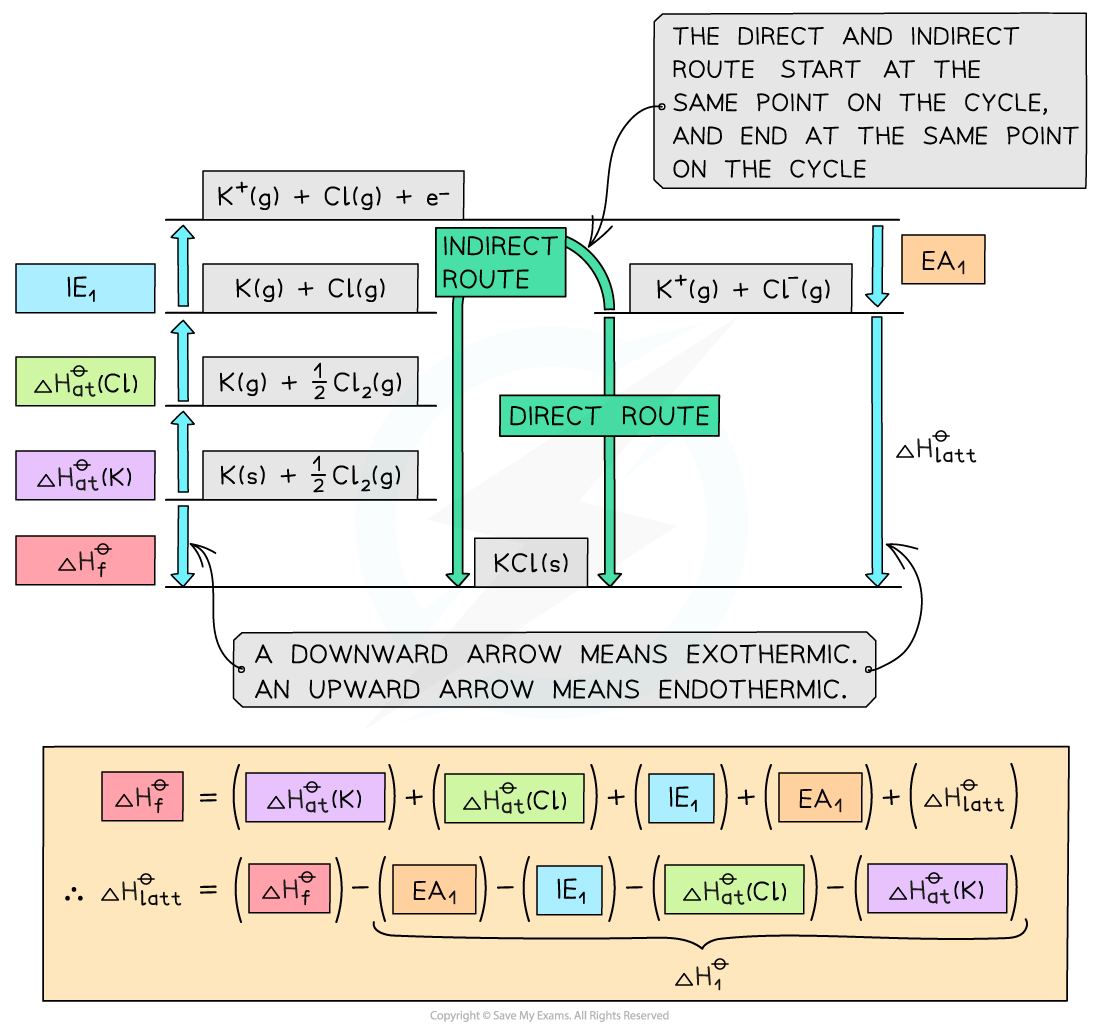
Worked Example
Constructing a Born-Haber cycle for MgO
Construct a Born-Haber Cycle which can be used to calculate the lattice energy of magnesium oxide

Answer
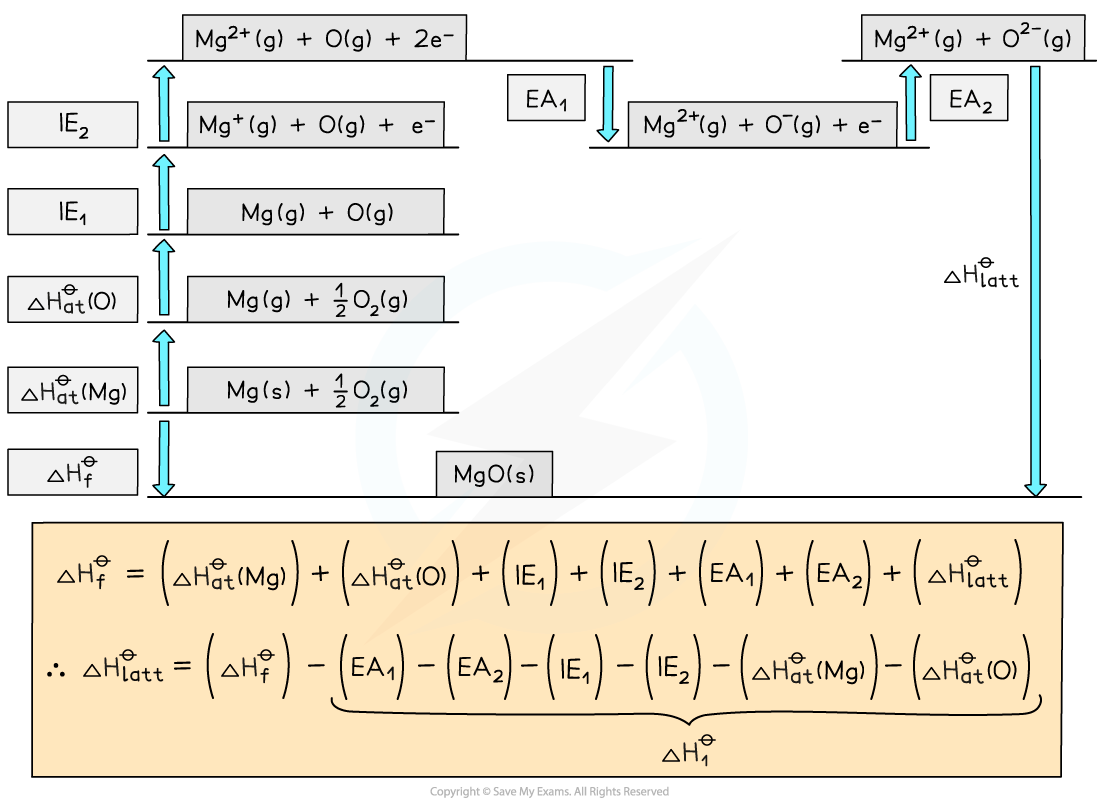
Born-Haber Cycles - Calculations
Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlattꝋ) by applying Hess’s law and rearranging:
ΔfHꝋ = ΔatHꝋ + ΔatHꝋ + IE + EA + ΔlattHꝋ
If we simplify this into three terms, this makes the equation easier to see:
ΔHlattꝋ
ΔHfꝋ
ΔH1ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
The simplified equation becomes
ΔfHꝋ = Δ1Hꝋ + ΔlattHꝋ
So, if we rearrange to calculate the lattice energy, the equation becomes
ΔlattHꝋ = ΔfHꝋ - Δ1Hꝋ
When calculating the ΔHlattꝋ, all other necessary values will be given in the question
A Born-Haber cycle could be used to calculate any stage in the cycle
For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
The principle would be exactly the same
Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl- ions
Worked Example
Calculating the lattice energy of KCl
Given the data below, calculate the ΔlattHꝋ of potassium chloride (KCl)

Answer
Step 1: The corresponding Born-Haber cycle is:

Step 2: Applying Hess’ law, the lattice energy of KCl is:
ΔlattHꝋ = ΔfHꝋ - Δ1Hꝋ
ΔlattHꝋ = ΔfHꝋ - [(ΔatHꝋ K) + (ΔatHꝋ Cl) + (IE1 K) + (EA1 Cl)]
Step 3: Substitute in the numbers:
ΔlattH = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol-1
Worked Example
Calculating the lattice energy of MgO
Given the data below, calculate the of ΔlattHꝋ magnesium oxide of magnesium oxide (MgO)

Answer
Step 1: The corresponding Born-Haber cycle is:

Step 2: Applying Hess’ law, the lattice energy of MgO is:
ΔlattHꝋ = ΔfHꝋ - Δ1Hꝋ
ΔlattHꝋ = ΔfHꝋ - [(ΔatHꝋ Mg) + (ΔatHꝋ O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]
Step 3: Substitute in the numbers:
ΔlattHꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
= -3812 kJ mol-1

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?