The Bacterial Growth Curve (Edexcel International A Level Biology): Revision Note

The Bacterial Growth Curve

• Bacteria divide using the process of binary fission during which one cell will divide into two identical cells

• The process is as follows

  • The single, circular DNA molecule undergoes DNA replication

  • Any plasmids present undergo DNA replication

  • The parent cell divides into two cells, with the cytoplasm roughly halved between the two daughter cells

  • The two daughter cells each contain a single copy of the circular DNA molecule and a variable number of plasmids

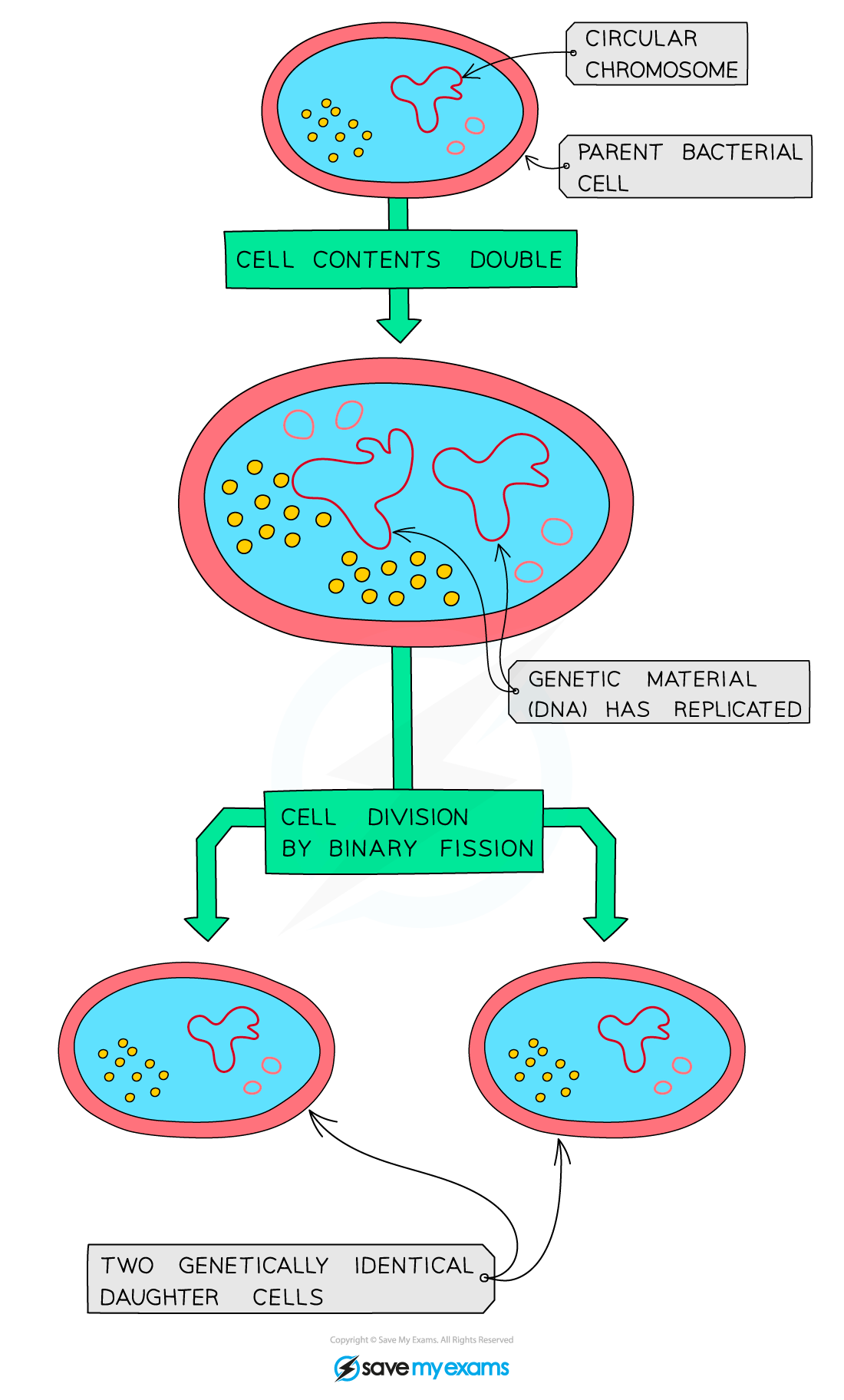
The process of binary fission produces two identical daughter cells

Bacterial growth curve

• The growth of a bacterial population follows a specific pattern over time; this is known as a growth curve

• There are 4 phases in the population growth curve of a microorganism population

  • Lag phase

    • The population size increases slowly as the microorganism population adjusts to its new environment and gradually starts to reproduce

  • Exponential phase

    • With high availability of nutrients and plenty of space, the population moves into exponential growth; this means that the population doubles with each division

    • This phase is also known as the log phase

  • Stationary phase 

    • The population reaches its maximum as it is limited by its environment, e.g. a lack of resources and toxic waste products.

    • During this phase the number of microorganisms dying equals the number being produced by binary fission and the growth curve levels off

  • Death phase

    • Due to lack of nutrients and a build up of toxic waste build up, death rate exceeds rate of reproduction and the population starts to decline

    • This phase is also known as the decline phase 

There are four phases in the standard growth curve of a microorganism

Using logarithms in growth curves

• During the exponential growth phase bacterial colonies can grow at rapid rates with very large numbers of bacteria produced within hours

• Dealing with experimental data relating to large numbers of bacteria can be difficult when using traditional linear scales

  • There can be a wide range of numbers reaching from single figures into millions

  • This makes it hard to work out a suitable scale for the axes of graphs

• Logarithmic scales can be very useful when investigating bacteria or other microorganisms

  • The numbers in a logarithmic scale represents logarithms, or powers, of a base number

  • If using a log₁₀ scale, in which the base number is 10, the numbers on the y-axis represent a power of 10, e.g. 1=10¹ (10), 2=10² (100), 3=10³ (1000) etc.

• Logarithmic scales allow for a wide range of values to be displayed on a single graph

• For example, if yeast cells were grown in culture over several hours the number of cells would increase very rapidly from the original number of cells present

• The results from such an experiment are shown in the graph below using a log scale

  • The number of yeast cells present at each time interval was converted to a logarithm before being plotted on the graph

    • This can be done using a log function on a calculator

  • The log scale is easily identifiable as there are not equal intervals between the numbers on the y-axis

  • The wide range of cell numbers fit easily onto the same scale

When a log₁₀ scale is used, the scale increases by a factor of 10 each time; this allows large increases in numbers to be shown on a single graph

Exponential growth rate constants

• To calculate the number of bacteria in a population the following formula can be used

• Where

  • N_t = the number of organisms at time t

  • N₀ = the number of organisms at time 0

  • k = the exponential growth rate constant

  • t = the time for which the colony has been growing

• To use this equation the exponential growth rate constant k must be calculated

  • This refers to the number of times the population doubles in a given time period

• The following formula can be used to calculate the exponential growth rate constant