Acceleration (Edexcel IGCSE Science (Double Award))

Revision Note

Test yourself

Author

Ashika

Last updated

5 December 2024

Did this video help you?

Acceleration

Rate of change in velocity

Acceleration is defined as the rate of change in velocity
- In other words, it describes how much an object's velocity changes every second
The equation below is used to calculate the average acceleration of an object:

$acceleration = \frac{change in velocity}{time taken}$

$a = \frac{∆ v}{t}$

Where:
- $a$ = acceleration in metres per second squared (m/s²)
- $∆ v$ = change in velocity in metres per second (m/s)
- $t$ = time taken in seconds (s)

Formula triangle for acceleration, change in velocity and time

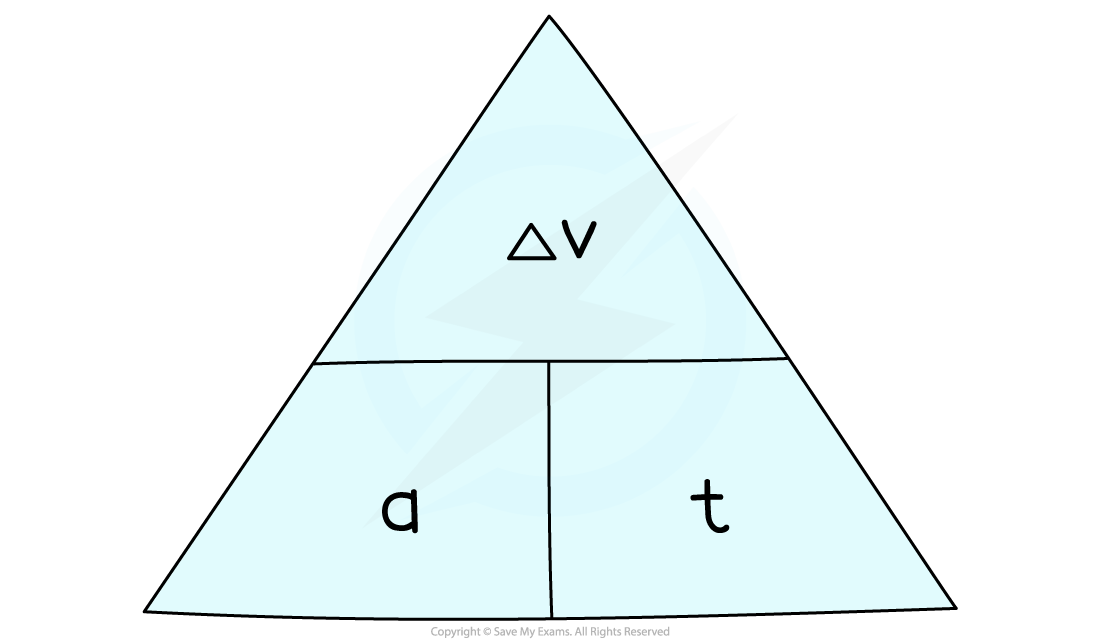
Acceleration Formula Triangle, downloadable IGCSE & GCSE Physics revision notes

To use an equation triangle, simply cover up the value you wish to calculate and the structure of the equation will be revealed

The change in velocity is found by the difference between the initial and final velocity:

$change in velocity = final velocity - initial velocity$

$∆ v = v - u$

Where:
- $v$ = final velocity in metres per second (m/s)
- $u$ = initial velocity in metres per second (m/s)
Therefore, the acceleration, or the rate of change in velocity, equation can be written as:

$a = \frac{(v - u)}{t}$

Speeding up and slowing down

An object that speeds up is accelerating
An object that slows down is decelerating
The acceleration of an object can be positive or negative, depending on whether the object is speeding up or slowing down
- If an object is speeding up, its acceleration is positive
- If an object is slowing down, its acceleration is negative (also known as deceleration)

Examples of acceleration and deceleration

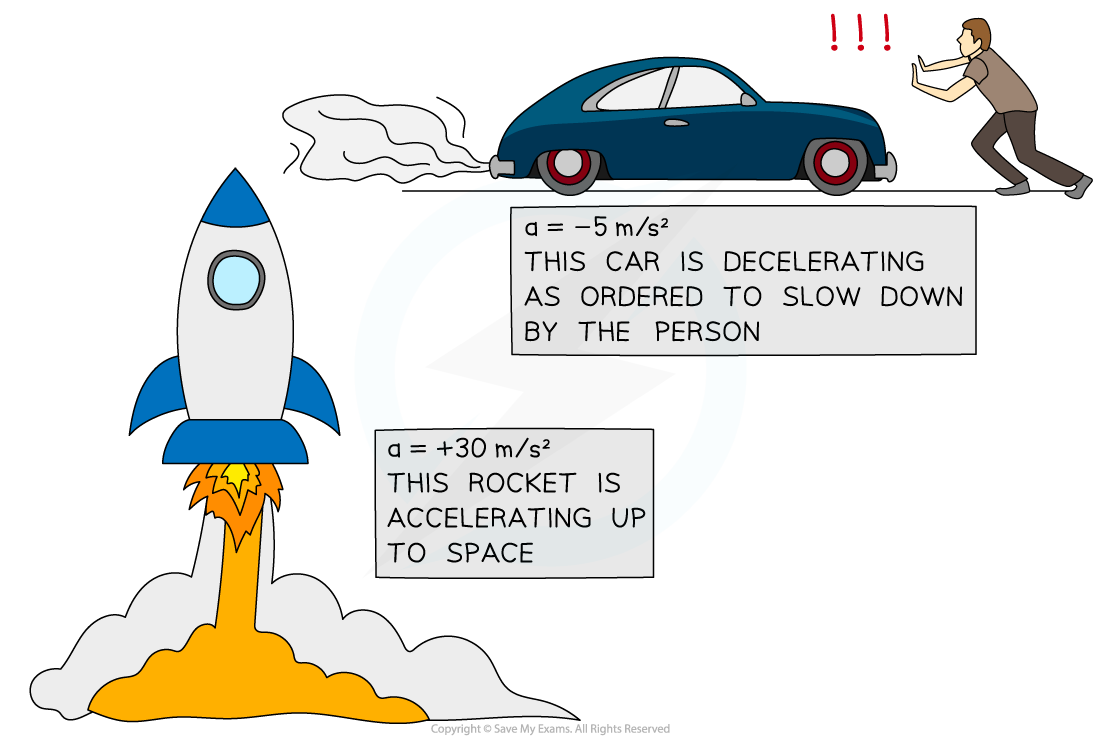
Acceleration Examples, downloadable IGCSE & GCSE Physics revision notes

A rocket speeding up (accelerating) and a car slowing down (decelerating)

Worked Example

A Japanese bullet train decelerates at a constant rate in a straight line. The velocity of the train decreases from 50 m/s to 42 m/s in 30 seconds.

(a) Calculate the change in velocity of the train.

(b) Calculate the deceleration of the train, and explain how your answer shows the train is slowing down.

Answer:

Part (a)

Step 1: List the known quantities

Initial velocity, $u = 50 m / s$
- Final velocity, $v = 42 m / s$

Step 2: Write the relevant equation

$∆ v = v - u$

Step 3: Substitute values for final and initial velocity

$∆ v = 42 - 50$

$∆ v = - 8 m / s$

Part (b)

Step 1: List the known quantities

Change in velocity, $∆ v = - 8 m / s$
- Time taken, $t = 30 s$

Step 2: Write the relevant equation

$a = \frac{(v - u)}{t} = \frac{∆ v}{t}$

Step 3: Substitute the values for change in velocity and time

$a = \frac{- 8}{30}$

$a = - 0.27 m / s^{2}$

Step 4: Interpret the value for deceleration

The answer is negative, which indicates the train is slowing down

Examiner Tips and Tricks

Remember, the units for acceleration are metres per second squared, m/s²

In other words, acceleration measures how much the velocity (in m/s) changes every second, m/s/s.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: