Resistors in Series (Edexcel IGCSE Science (Double Award))

The combined resistance R in the following series circuit is 60 Ω.

What is the resistance value of R₂?

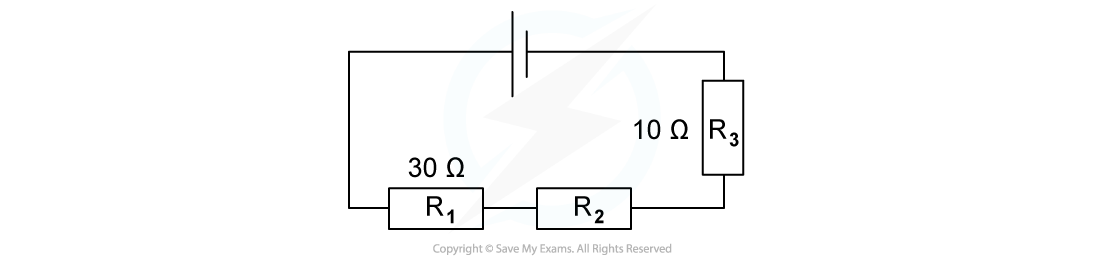
A     100 Ω               B     30 Ω               C     20 Ω               D     40 Ω

ANSWER:  C

Step 1: Write down the equation for the combined resistance in series

Step 2: Substitute the values for total resistance R and the other resistors

60 Ω = 30 Ω + R₂ + 10 Ω

Step 3: Rearrange for R₂

R₂ = 60 Ω – 30 Ω – 10 Ω = 20 Ω

Dennis sets up a series circuit as shown below.

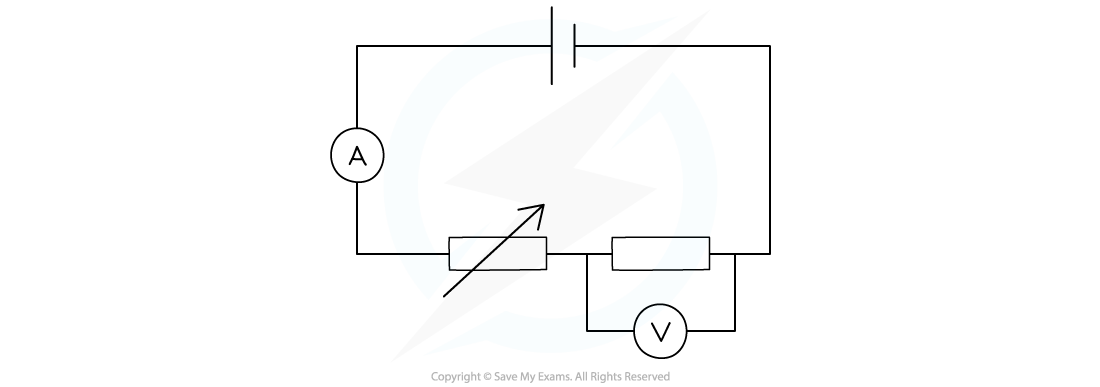
The cell supplies a current of 2 A to the circuit, and the fixed resistor has a resistance of 4 Ω.

(a) How much current flows through the fixed resistor?

(b) What is the reading on the voltmeter?

Answer:

Part (a)

Step 1: Recall that current is conserved in a series circuit

• Since current is conserved in a series circuit, it is the same size if measured anywhere in the series loop

• This means that since the cell supplies 2 A to the circuit, the current is 2 A everywhere

• Therefore, 2 A flows through the fixed resistor

Part (b)

Step 1: List the known quantities

• Current, I = 2 A

• Resistance, R = 4 Ω

Step 2: State the equation linking potential difference, resistance and current

• The equation linking potential difference, resistance and current is:

Step 3: Substitute the known values into the equation and calculate the potential difference

V = 2 × 4 = 8 V

• Therefore, the voltmeter reads 8 V across the fixed resistor