IGCSEScienceEdexcelScience (Double Award)PhysicsRevision Notes5. Solids, Liquids & GasesIdeal GasesBoyle's Law

Boyle's Law (Edexcel IGCSE Science (Double Award): Physics): Revision Note

Exam code: 4SD0

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on 2 July 2026

Boyle's law

For a fixed mass of a gas held at a constant temperature, the Boyle's law formula is:

pV = constant

Where:
- p = pressure in pascals (Pa)
- V = volume in metres cubed (m³)

This means that the pressure and volume are inversely proportional to each other
- When the volume decreases (compression), the pressure increases
- When the volume increases (expansion), the pressure decreases

This is because when the volume decreases, the same number of particles collide with the walls of a container but more frequently as there is less space
- However, the particles still collide with the same amount of force meaning greater force per unit area (pressure)
The key assumption is that the temperature and the mass (and number) of the particles remains the same

Gas Laws Molecular Model (1), downloadable AS & A Level Physics revision notes

Increasing the volume of a gas decreases its pressure

This equation can also be rewritten for comparing the pressure and volume before and after a change in a gas:

p₁V₁ = p₂V₂

Where:
- p₁= initial pressure in pascals (Pa)
- V₁= initial volume in metres cubed (m³)
- p₂= final pressure in pascals (Pa)
- V₂= final volume in metres cubed (m³)

This equation is sometimes referred to as Boyle's Law

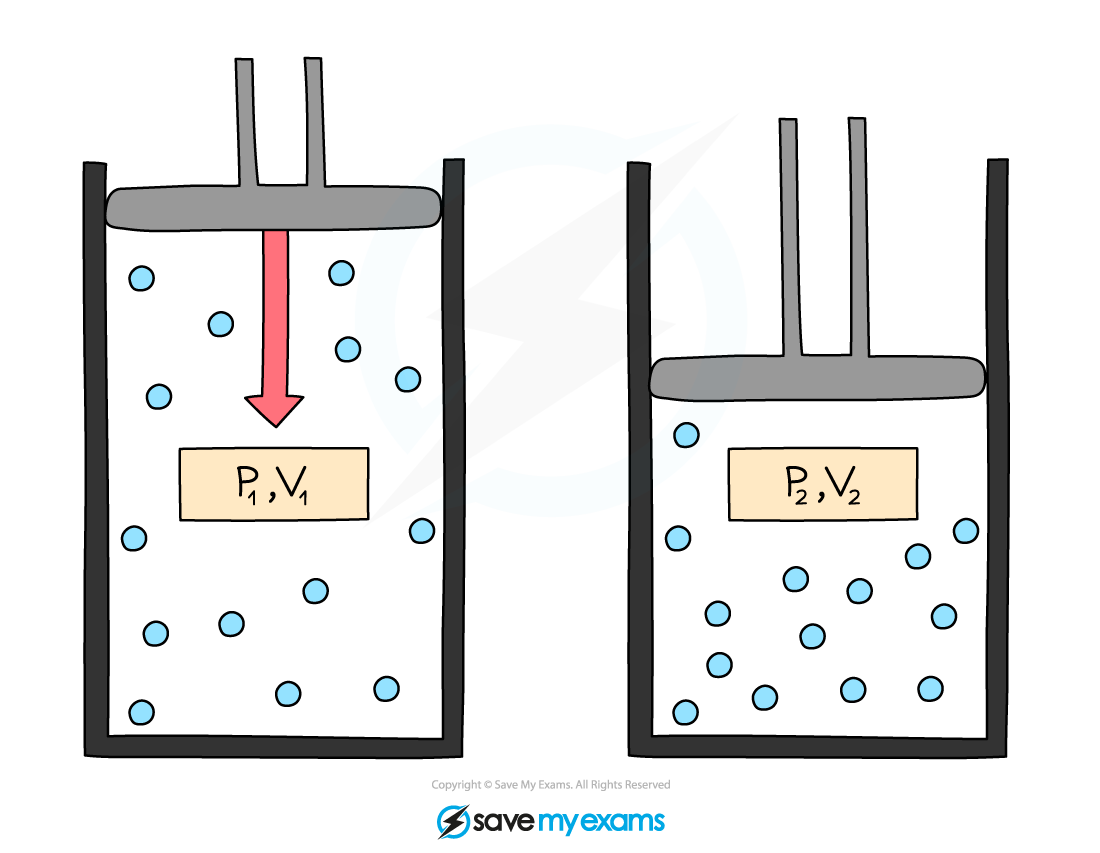
Pressure-vs-Volume, IGCSE & GCSE Physics revision notes

Initial pressure and volume, p₁ and V₁, and final pressure and volume, p₂ and V₂. When volume decreases, pressure increases

Worked Example

A gas occupies a volume of 0.70 m³ at a pressure of 200 Pa. Calculate the pressure exerted by the gas if it is compressed to a volume of 0.15 m³.Assume that the temperature and mass of the gas stay the same.

Answer:

Step 1: List the known quantities

Initial volume, V₁ = 0.70 m³
Initial pressure, p₁ = 200 Pa
Final volume, V₂ = 0.15 m³

Step 2: Write the relevant equation

$p_{1} V_{1} = p_{2} V_{2}$

Step 3: Rearrange for the final pressure, p₂

Divide both sides by V₂ to get the p₂ term on its own

$\frac{p_{1} V_{1}}{V_{2}} = \frac{p_{2} V_{2}}{V_{2}}$

$\frac{p_{1} V_{1}}{V_{2}} = p_{2}$

Step 4: Substitute in the values

$p_{2} = \frac{p_{1} V_{1}}{V_{2}} = \frac{200 \times 0.70}{0.15}$

$p_{2} = 930 Pa$ (2 s.f.)

Examiner Tips and Tricks

Always check whether your final answer makes sense. If the gas has been compressed, the final pressure is expected to be more than the initial pressure (like in the worked example). If this is not the case, double-check the rearranging of any formulae and the values put into your calculator.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent