Boyle's Law (Edexcel IGCSE Physics (Modular)) : Revision Note
Boyle's law
For a fixed mass of a gas held at a constant temperature, the Boyle's law formula is:
pV = constant
Where:
p = pressure in pascals (Pa)
V = volume in metres cubed (m3)
This means that the pressure and volume are inversely proportional to each other
When the volume decreases (compression), the pressure increases
When the volume increases (expansion), the pressure decreases
This is because when the volume decreases, the same number of particles collide with the walls of a container but more frequently as there is less space
However, the particles still collide with the same amount of force meaning greater force per unit area (pressure)
The key assumption is that the temperature and the mass (and number) of the particles remains the same
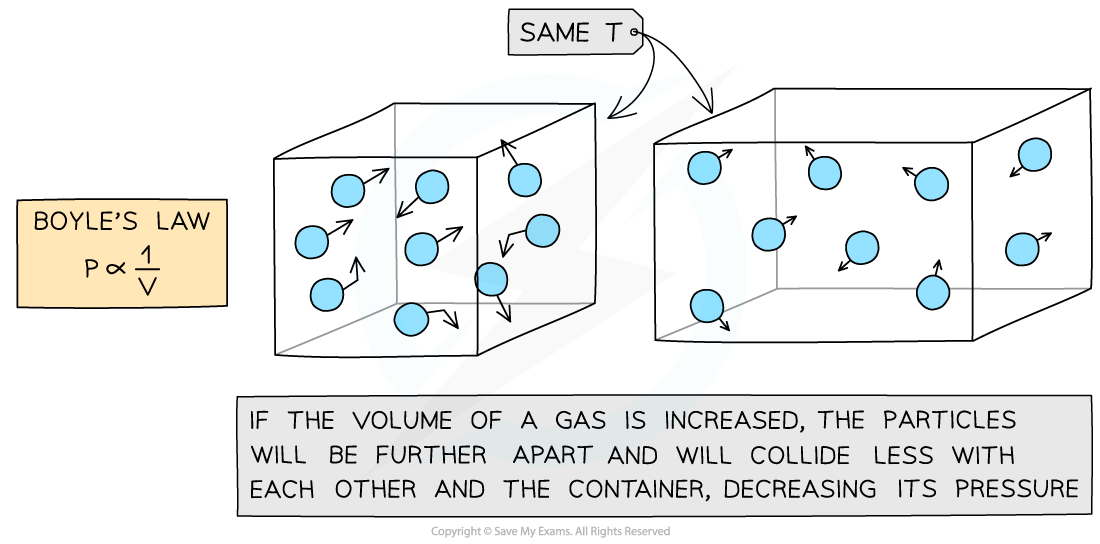
Increasing the volume of a gas decreases its pressure
This equation can also be rewritten for comparing the pressure and volume before and after a change in a gas:
p1V1 = p2V2
Where:
p1 = initial pressure in pascals (Pa)
V1 = initial volume in metres cubed (m3)
p2 = final pressure in pascals (Pa)
V2 = final volume in metres cubed (m3)
This equation is sometimes referred to as Boyle's Law
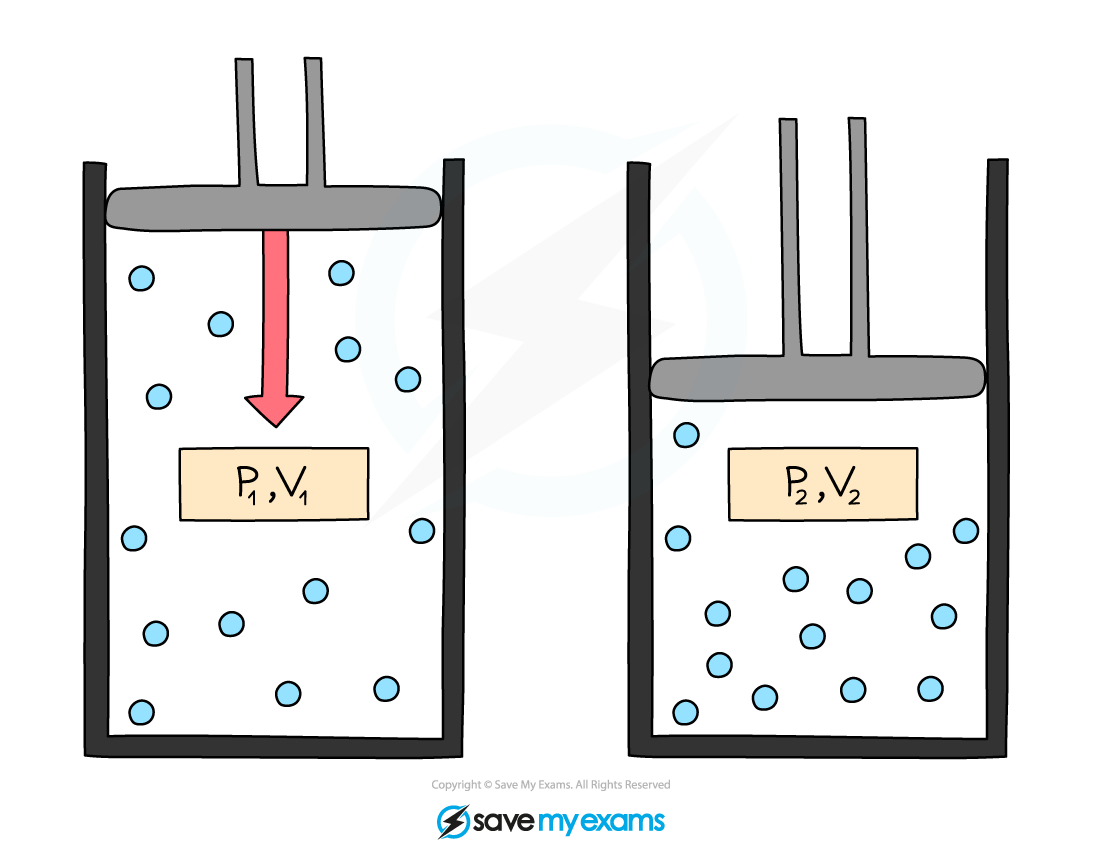
Initial pressure and volume, p1 and V1, and final pressure and volume, p2 and V2. When volume decreases, pressure increases
Worked Example
A gas occupies a volume of 0.70 m3 at a pressure of 200 Pa. Calculate the pressure exerted by the gas if it is compressed to a volume of 0.15 m3.Assume that the temperature and mass of the gas stay the same.
Answer:
Step 1: List the known quantities
Initial volume, V1 = 0.70 m3
Initial pressure, p1 = 200 Pa
Final volume, V2 = 0.15 m3
Step 2: Write the relevant equation
Step 3: Rearrange for the final pressure, p2
Divide both sides by V2 to get the p2 term on its own
Step 4: Substitute in the values
(2 s.f.)
Examiner Tips and Tricks
Always check whether your final answer makes sense. If the gas has been compressed, the final pressure is expected to be more than the initial pressure (like in the worked example). If this is not the case, double-check the rearranging of any formulae and the values put into your calculator.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

