IGCSEPhysicsEdexcelPhysics (Modular)Unit 1Revision Notes1. Forces & MotionForces, Movement & Changing ShapeUnbalanced Forces

Unbalanced Forces (Edexcel IGCSE Physics (Modular))

Revision Note

Test yourself
Ashika

Written by: Ashika

Reviewed by: Caroline Carroll

Unbalanced forces

  • When multiple forces act on a single object, the forces can be added together to produce a resultant force

  • When the forces acting on an object completely cancel out

    • the forces are balanced

    • the resultant force is zero

  • When the forces acting on an object do not completely cancel out

    • the forces are unbalanced

    • there is a resultant force

Balanced forces

  • Balanced forces mean that the forces have combined in such a way that they cancel each other out and no resultant force acts on the body

    • For example, the weight of a book on a desk is balanced by the normal force of the desk

    • As a result, no resultant force is experienced by the book, the book and the table are equal and balanced

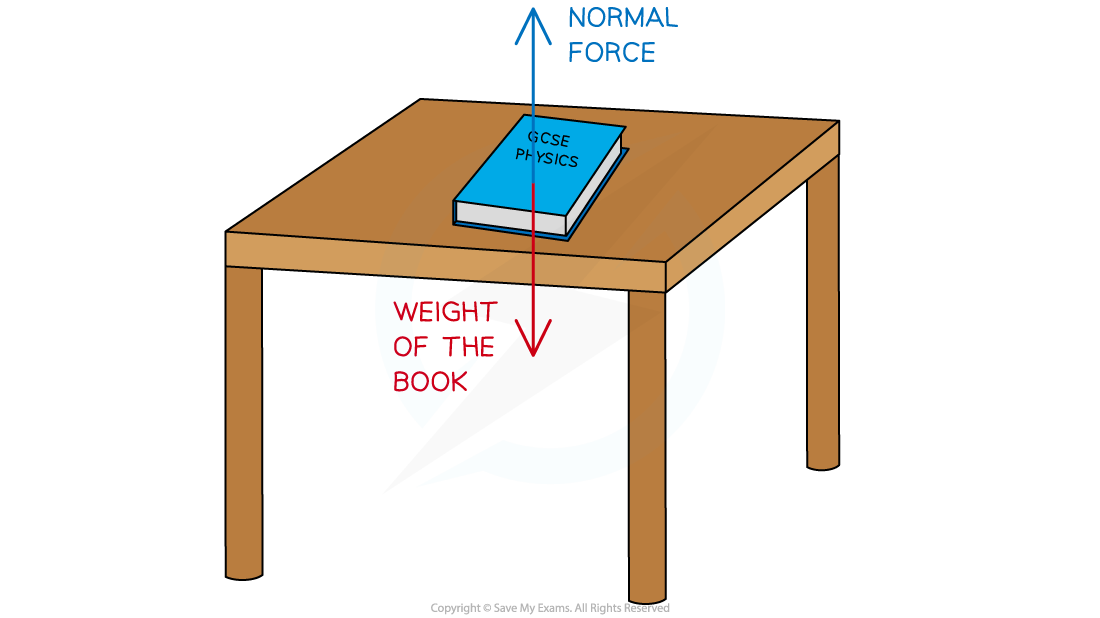
Balanced Forces, downloadable IGCSE & GCSE Physics revision notes

A book resting on a table is an example of balanced forces

Unbalanced forces

  • Unbalanced forces mean that the forces have combined in such a way that they do not cancel out completely and there is a resultant force on the object

    • For example, imagine two people playing a game of tug-of-war, working against each other on opposite sides of the rope

    • If person A pulls with 80 N to the left and person B pulls with 100 N to the right, these forces do not cancel each other out completely

    • Since person B pulled with more force than person A the forces will be unbalanced and the rope will experience a resultant force of 20 N to the right

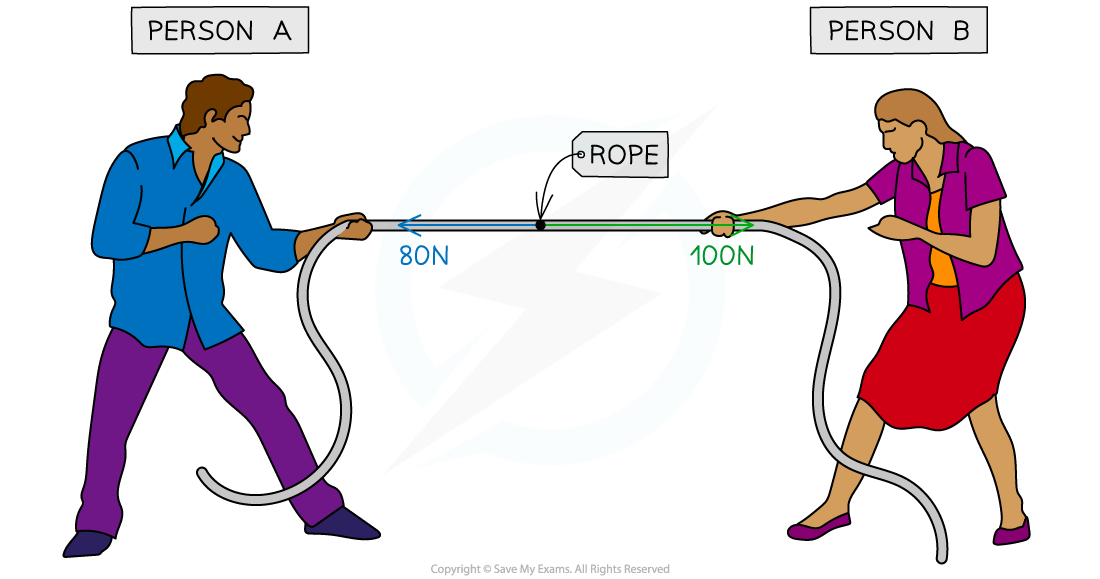
Tug O War, downloadable IGCSE & GCSE Physics revision notes

A tug-of-war is an example of when forces can become unbalanced

Unbalanced Forces, Mass & Acceleration

  • When forces combine on an object in such a way that they do not cancel out, there is a resultant force on the object

  • This resultant force causes the object to accelerate (i.e. change its velocity)

    • The object might speed up

    • The object might slow down

    • The object might change direction

  • The relationship between resultant force, mass and acceleration is given by the equation:

F = m × a

  • Where:

    • F = resultant force, measured in newtons (N)

    • m = mass, measured in kilograms (kg)

    • a = acceleration, measured in metres per second squared (m/s2)

  • This equation is also known as Newton's second law of motion

Worked Example

A car salesperson claims that their best car has a mass of 900 kg and can accelerate from 0 to 27 m/s in 3 seconds.

Calculate:

a) The acceleration of the car in the first 3 seconds.

b) The force required to produce this acceleration.

Answer:

Part (a)

Step 1: List the known quantities

  • Initial velocity = 0 m/s

  • Final velocity = 27 m/s

  • Time, t = 3 s

Step 2: State the equation for acceleration

a space equals space fraction numerator open parentheses v space minus space u close parentheses over denominator t end fraction

Step 3: Calculate the acceleration

a space equals space fraction numerator open parentheses 27 space minus space 0 close parentheses over denominator 3 end fraction

a space equals space 9 space straight m divided by straight s squared

Part (b)

Step 1: List the known quantities

  • Mass of the car, m = 900 kg

  • Acceleration, a = 9 m/s2

Step 2: Identify which law of motion to apply

  • The question involves quantities of force, mass and acceleration, so Newton's second law is required:

F space equals space m a

Step 3: Calculate the force required to accelerate the car

F space equals space 900 space cross times space 9

F space equals space 8100 space straight N

Worked Example

A passenger of mass 70 kg travels in a car at a speed of 20 m/s. The vehicle is involved in a collision, which brings the car (and the passenger) to a halt in 0.1 seconds.

Calculate:

a) The deceleration of the car (and the passenger).

b) The decelerating force on the passenger.

Answer:

Part (a)

Step 1: List the known quantities

  • Initial velocity, u = 20 m/s

  • Final velocity, v = 0 m/s

  • Time, t = 0.1 s

Step 2: Write out the equation for acceleration

a space equals space fraction numerator open parentheses v space minus space u close parentheses over denominator t end fraction

Step 3: Calculate the deceleration of the car (and the passenger):

a space equals space fraction numerator open parentheses 0 space minus space 20 close parentheses over denominator 0.1 end fraction

a space equals space fraction numerator negative 20 over denominator 0.1 end fraction

a space equals space minus 200 space straight m divided by straight s squared

Part (b)

Step 1: List the known quantities

  • Mass of the passenger, m = 70 kg

  • Acceleration (deceleration, in this case), a = −200 m/s2

Step 2: State the relationship between resultant force, mass and acceleration

  • This question involves quantities of force, mass and acceleration, so the appropriate equation for this case is:

F space equals space m a

Step 3: Calculate the decelerating force

F space equals space 70 space cross times space open parentheses negative 200 close parentheses

F space equals space minus 14 space 000 space straight N

Examiner Tips and Tricks

Remember that the resultant force is a vector quantity. Examiners may ask you to comment on why its value is negative - this happens when the resultant force acts in the opposite direction to the object's motion. In the worked example above, the resultant force opposes the passenger's motion, slowing them down (decelerating them) to a halt, this is why it has a minus symbol.

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Resultant ForcesNext:Weight
    Author
    Reviewer
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.