Half-Life (CIE IGCSE Physics: Co-ordinated Sciences (Double Award))

• The half-life of a particular isotope is defined as:

the time taken for half the nuclei of that isotope in any sample to decay

• The rate at which the activity of a sample decreases is measured in terms of half-life
  • This is the time it takes for the activity of a sample to fall to half its original level

• This is the time it takes for the activity of the sample to decrease from 100 % to 50 %
  • It is the same length of time as it would take to decrease from 50 % activity to 25 % activity

• Different isotopes have different half-lives and half-lives can vary from a fraction of a second to billions of years in length
  • The half-life is constant for a particular isotope

Representing half life

• Half-life can be determined from an activity–time graph

A half-life graph

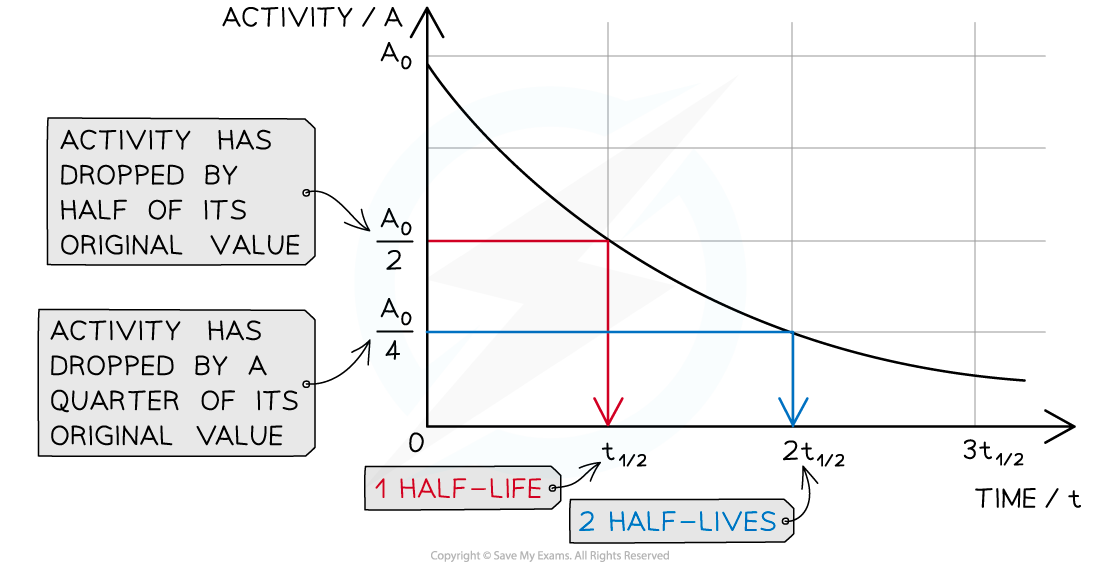
The graph shows how the activity of a radioactive sample changes over time. Each time the original activity halves, another half-life has passed

• Half-life can also be represented on a table
  • As the number of the half-life increases, the proportion of the isotope remaining halves

Table showing the number of half-lives to the proportion of isotope remaining

Number of half-lives	Proportion of isotope remaining
0	1
1
2
3
4
...	...