Speed-Time Graphs

Did this video help you?

A speed-time graph is used to describe the speed of an object and calculate its acceleration

Constant acceleration on a speed-time graph

If an object is moving at a constant acceleration, the speed-time graph will be a straight line
- If the constant acceleration is zero, the line will be horizontal
- If the constant speed is non-zero, the line will have a gradient

If an object has an acceleration of zero, the object is travelling at a constant velocity
- Its velocity is not changing over time
- If the constant speed is zero, then the object is stationary

Motion on a speed-time graph

1-2-4-speed-time-graph-2-cie-igcse-23-rn

This image shows how to interpret the slope of a speed-time graph

The gradient of a speed-time graph represents the object's acceleration
- A steeper slope, or a higher gradient, represents a greater acceleration
- A shallower slope, or a lower gradient, represents a slower acceleration

If the gradient is positive, the line slopes upward
- A positive gradient represents an increasing speed, or acceleration

If the gradient is negative, the line slopes downward
- A negative gradient represents a decreasing speed, or deceleration

Speeding up and slowing down on a speed-time graph

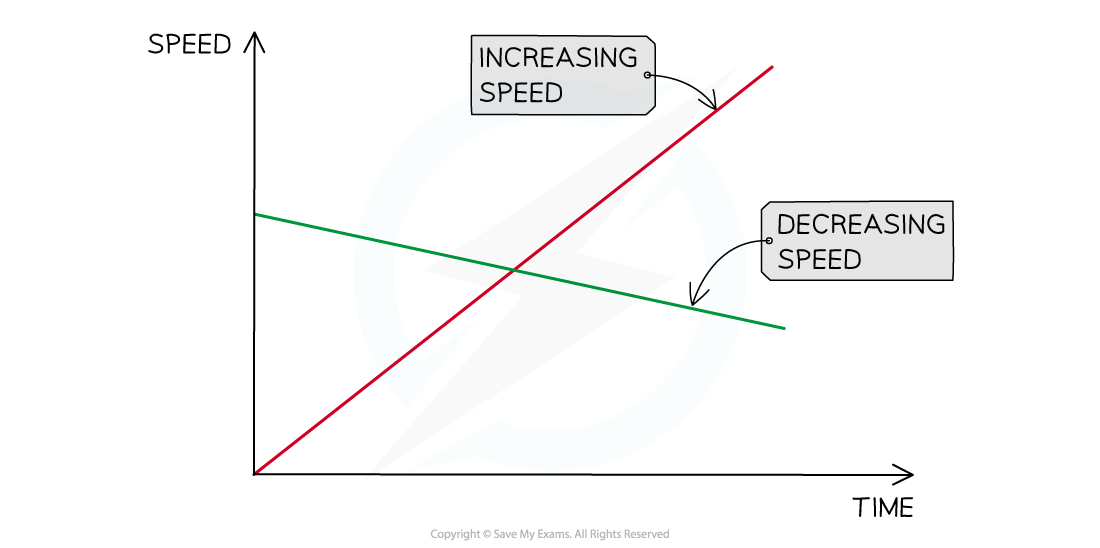
1-2-4-speed-time-graph-cie-igcse-23-rn

Both of these objects are moving at a constant acceleration, because the lines are straight. The positive gradient represents an increasing speed or positive acceleration. The negative gradient represents a decreasing speed or negative acceleration.

Examiner Tip

For CIE IGCSE Physics, you may be asked plot a graph of your own, or to interpret information given to you in a graph. You can read more about graph skills in the article Graph skills in GCSE Physics

Calculating distance from speed-time graphs

Speed-time graphs can also be used to determine the distance travelled by an object

The area under a speed-time graph

The area under a speed-time graph represents the distance travelled

area-under-speed-time-graph

The area under a speed-time graph represents the distance travelled

If the area of a section of the speed-time graph forms a triangle, the area can be calculated using:

$A_{T} = \frac{1}{2} b h$

If the area of a section of the speed-time graph forms a rectangle, the area can be determined using:

$A_{R} = b h$

Where:
- $A_{T}$ = area of a triangle
- $A_{R}$ = area of a rectangle
- $b$ = base
- $h$ = height

The total distance travelled can be determined by finding the total area under the speed-time graph
The distance travelled for part of the journey can be determined by finding the area under the graph for a specific time interval

Area under a speed-time graph split into sections

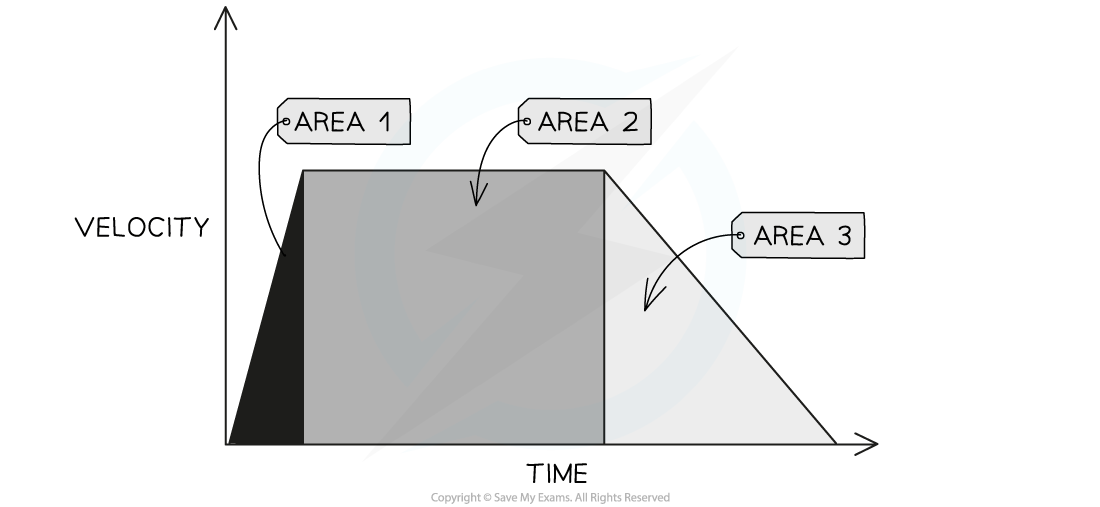
The area under a speed-time graph can split into triangular and rectangular sections

Worked example

The speed-time graph below shows a car journey that lasts for 160 seconds.

1-2-4-worked-eg-1-cie-igcse-23-rn

Calculate the total distance travelled by the car on this journey.

Answer:

Step 1: Recall that the area under a velocity-time graph represents the distance travelled

In order to calculate the total distance travelled, the total area underneath the line must be determined

Step 2: Identify each enclosed area

In this example, there are five enclosed areas under the line
These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:

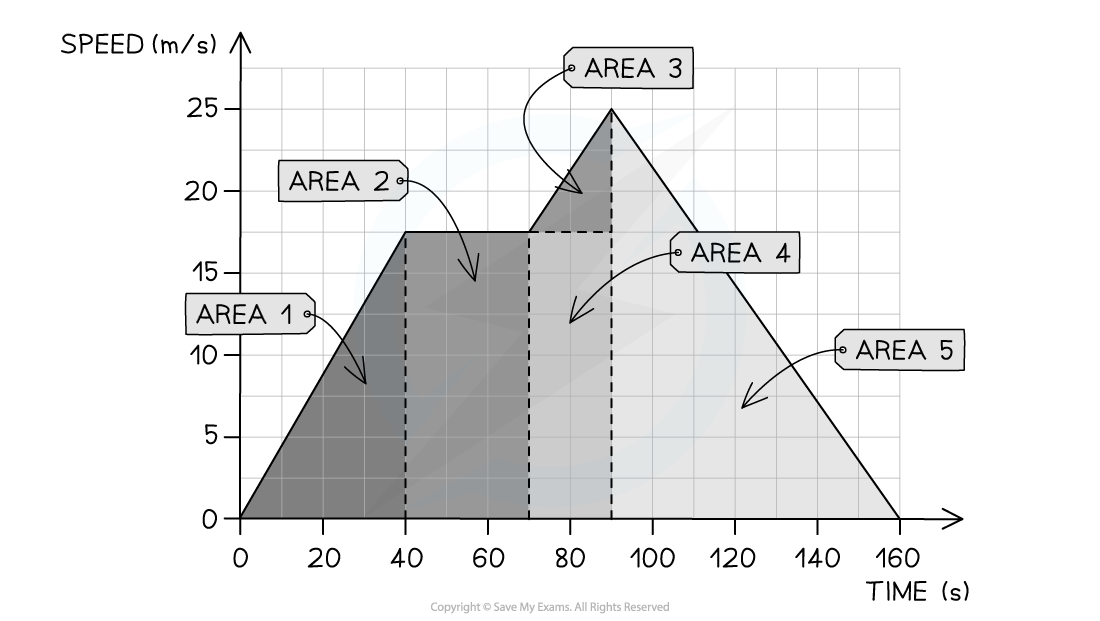
1-2-4-worked-eg-2-cie-igcse-23-rn

Step 3: Calculate the area of each enclosed shape under the line

Area 1 = area of a triangle

$A_{1} = \frac{1}{2} b h$

$A_{1} = \frac{1}{2} \times 40 \times 17.5$

$A_{1} = 350 m$

Area 2 = area of a rectangle

$A_{2} = b h$

$A_{2} = 30 \times 17.5$

$A_{2} = 525 m$

Area 3 = area of a triangle

$A_{3} = \frac{1}{2} b h$

$A_{3} = \frac{1}{2} \times 20 \times 7.5$

$A_{3} = 75 m$

Area 4 = area of a rectangle

$A_{4} = b h$

$A_{4} = 20 \times 17.5$

$A_{4} = 350 m$

Area 5 = area of a triangle

$A_{5} = \frac{1}{2} b h$

$A_{5} = \frac{1}{2} \times 70 \times 25$

$A_{5} = 875 m$

Step 4: Calculate the total distance travelled by finding the total area under the line

Add up each of the five areas enclosed:

$total distance = A_{1} + A_{2} + A_{3} + A_{4} + A_{5}$

$total distance = 350 + 525 + 75 + 350 + 875$

$total distance = 2175 m$

Examiner Tip

Some areas will need to be split into a triangle and a rectangle to determine the area for a specific time interval, like areas 3 & 4 in the worked example above.

If you are asked to find the distance travelled for a specific time interval, then you just need to find the area of the section above that time interval.

For example, the distance travelled between 70 s and 90 s is the sum of Area 3 + Area 4

Speed-Time Graphs (CIE IGCSE Physics: Co-ordinated Sciences (Double Award))

Revision Note